Journal d'un Terrien
Web log de Serge Boisse
On line depuis 1992 !
http://sboisse.free.fr/programmation/Algorithmes/Probleme du sac a dos.php
Auteur : Serge Boisse
Un algorithme dynamique pour le problème du sac à dos
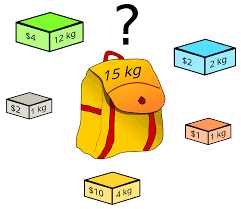
En algorithmique, le problème du sac à dos, parfois noté (KP) (de l'anglais Knapsack Problem)1 est un problème d'optimisation combinatoire. Ce problème classique en informatique et en mathématiques modélise une situation analogue au remplissage d'un sac à dos. Il consiste à trouver la combinaison d'éléments la plus précieuse à inclure dans un sac à dos, étant donné un ensemble d'éléments décrits par leurs poids et valeurs.
L'objectif du problème du sac à dos est de sélectionner des objets à mettre dans le sac à dos de façon à maximiser la somme des valeurs des objets pris, sous la contrainte que le poids total des objets pris ne dépasse pas la capacité du sac à dos. Ce problème est NP-complet. Ainsi, il est difficile à résoudre, en particulier pour les grands ensembles d'objets.
Cet algorithme trouve la solution optimale.
si
Le problème est toujours NP car pour qu'il soit P il faudrait une complexité
la vidéo
le code python
# Solution optimale - programmation dynamique
def sacADos_dynamique(capacite, elements):
matrice = [[0 for x in range(capacite + 1)] for x in range(len(elements) + 1)]
for i in range(1, len(elements) + 1):
for w in range(1, capacite + 1):
if elements[i-1][1] <= w:
matrice[i][w] = max(elements[i-1][2] + matrice[i-1][w-elements[i-1][1]], matrice[i-1][w])
else:
matrice[i][w] = matrice[i-1][w]
# Retrouver les éléments en fonction de la somme
w = capacite
n = len(elements)
elements_selection = []
while w >= 0 and n >= 0:
e = elements[n-1]
if matrice[n][w] == matrice[n-1][w-e[1]] + e[2]:
elements_selection.append(e)
w -= e[1]
n -= 1
return matrice[-1][-1], elements_selection
# --UTILISATION ---------------------------------
#exemple :
ele = [('Montre a gousset', 2, 6), # nom, poids, valeur
('Boule de bowling', 3, 10),
('Portrait de tata Germaine', 4, 12)]
# affiche la valeur totale et chaque élément choisi avec son poids et sa valeur
# le premier arg est la capacité (poids max) du sac à dos
print('Algo dynamique', sacADos_dynamique(5, ele)) # -> Algo dynamique (16, [('Boule de bowling', 3, 10), ('Montre a gousset', 2, 6)])
page créée le 18/03/2025 à 15:09modifiée le 02/06/2025 à 16:15
Commentaires (0) :
Page :Ajouter un commentaire (pas besoin de s'enregistrer)
En cliquant sur le bouton "Envoyer" vous acceptez les conditions suivantes : Ne pas poster de message injurieux, obscène ou contraire à la loi, ni de liens vers de tels sites. Respecter la "netiquette", ne pas usurper le pseudo d'une autre personne, respecter les posts faits par les autres. L'auteur du site se réserve le droit de supprimer un ou plusieurs posts à tout moment. Merci !Ah oui : le bbcode et le html genre <br>, <a href=...>, <b>b etc. ne fonctionnent pas dans les commentaires. C'est voulu.