Journal d'un Terrien
Web log de Serge Boisse
On line depuis 1992 !
Liste des tags :
__________________
http://sboisse.free.fr/science/maths/Mes Recherches mathematiques/Gagner contre le hasard ou la bourse.php
Gagner contre le hasard ou la bourse
Auteur : Serge Boisse
Voir aussi: _Vidéos maths(lien privé), Théorème de Bayes(lien privé) Les 100 prisonniers(lien privé) Les enveloppes
 Résumé : Est-il possible de gagner dans un jeu de type pile ou face ?
Résumé : Est-il possible de gagner dans un jeu de type pile ou face ?
Est-ce possible ?
Normalement, non, si l'espérance de gain E est négative ou nulle :
où
Par exemple à la roulette française, pour une mise
Mais le vrai monde est plus compliqué que la roulette...
un exemple
Supposons le jeu suivant :
On lance une pièce (truquée) en l'air. Si elle tombe sur face, vous gagnez 2/3 de votre mise. Sinon vous la perdez. Mais la pièce a 70% de chance de tomber sur face.
Vous misez 6 euros. L'espérance de gain est
Elle est positive, et vous décidez de jouer. Mais comment ? Supposons que vous savez que vous ne pourrez jouer que 100 fois. Comment maximiser le gain final ?
Supposons que votre stratégie soit de miser à chaque fois 5 euros. Les choses peuvent se passer de plein de façons différentes :
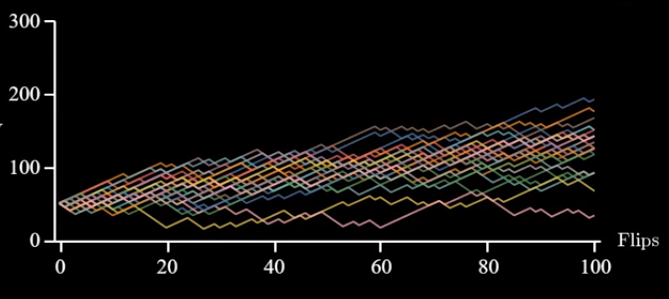
On peut comparer le gain final, ou le gain final ajusté par le risque, ou même passer le gain final dans une "fonction d'utilité".et utiliser l'utilité moyenne. D'autres choix sont possibles.
Le critère de Kelly
On choisira de calculer le taux d'accroissement moyen (growth rate en anglais)
ou en inversant,
Dans notre exemple ce la donnerait
On va effectuer un grand nombre de simulations en pondérant le taux
Mais plupart des gens sont très loin de tirer le profit maximal de ce jeu. il est en effet possible dans 94% des cas de décupler sa fortune !
quelle est alors la meilleure stratégie ?
Kelly affirme qu'elle consiste à miser un pourcentage (une fraction) fixe de sa fortune à chaque fois, et que cette fraction
où
Dans notre exemple,
Si une pièce truquée (p=0.6) permettait de gagner 100% de la mise, alors il faudrait miser
Si
A la bourse ?
Quand on achète une action à un prix
Le critère de Kelly devient
où
Notons que si le jeu est très en notre faveur (par exemple
on peut modéliser les fluctuations par un mouvement brownien...
Scholes et les options...
cf https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model
et
The Trillion Dollar Equation (video Youtube)
Kelly et les options
Une option call peut être réalisée ou pas : si elle l'est, on gagne la difference de prix
On est donc en droit d'appliquer le critère de Kelly. La partie de sa fortune qu'il faudrait "miser" à chaque achat d'option serait
Jeux à énigmes et paradoxes probabilistes
How Science is Taking the Luck out of Gambling (video Youtube)
Plusieurs idées intéressantes dans cette vidéo
- Lorsque on a un jeu du du style "choisir entre plusieurs chevaux sur lesquels miser", à probabilité de gain égales, il faut miser sur celui qui a la plus grande variabilité (ou dans une élection, le plus controversé)
Question
et si on a "3 chevaux", c'est à dire trois actions dont on normalise les valeurs, mais avec forcément des écarts-types différents ?
#TBC
poker simplifié :
- Dans un jeu comme "On distribue une seule carte piochée au hasard dans jeu de cartes classique à chacun des deux joueurs : chaque joueur mise 1 euro. Je gagne si j'ai une plus haute carte que mon adversaire ; à chaque tour je peux arrêter pour voir, ou renchérir, et c'est alors à mon adversaire de voir ou renchérir...", le premier joueur doit renchérir si il a une carte haute, et voir si c'est une carte moyenne. Mais si c'est une carte basse, il doit également renchérir car retourner sa carte maintenant signifierait perdre. En d'autres terme, il doit bluffer. (John von Neuman) cf http://datagenetics.com/blog/december32018/index.html
Les 3 portes
les enveloppes
évasion impossible (flip the coin)
Cas réel
En fait l'algo "Delahaye" pour les 3 portes ne marche si
Mais dans le cas de la bourse, en fait :
- on a deux actions A et B (on normalise leurs valeurs respectives pour être égales à t=0 )
- chaque action a une proba 1/2 de monter ou descendre.
- on fait la prédiction maintenant (t=0) que l'action A atteindra le montant
- En fait, il y a trois possibilités :
- soit les deux actions montent (proba 1/4)
- soit les deux actions descendent (proba 1/4)
- soit l'une monte et l'autre descend (proba 1/2)
autres paradoxes de probabilité
Et les stratégies de prisonniers ? cf https://www.youtube.com/watch?v=iSNsgj1OCLA (100 prisonniers et 100 boîtes). Voir mon analyse ici : Les 100 prisonniers(lien privé)
On pourrait imaginer
La #bourse
En fait si l'on suppose qu'une action a une chance sur 2 de monter ou de descendre, j'ai six choix possibles :
- ne rien faire
- acheter l'action
- acheter une option call (si je pense que l'action va monter de plus que le prix de l'option)
- acheter une option put (si je pense que l'action va descendre)
- acheter l'action et une option call
- acheter l'action et une option put (si je pense que l'action va descendre)
En réalité c'est encore plus compliqué à cause des ordres à cours limite, des types d'ordre stop loss, take profit etc.
stratégie temporelle pour la bourse
On pourrait imaginer que j'ai le choix entre
à t=0; j'en choisis une, disons
à t=1, je remarque que l'une de celle que je n'ai pas choisie (disons
à t=2 je récolte le le fruit de ma stratégie.
#TBC
Voir aussi :
page créée le 18/03/2025 à 15:09modifiée le 11/03/2025 à 20:58
Commentaires (0) :
Page :Ajouter un commentaire (pas besoin de s'enregistrer)
En cliquant sur le bouton "Envoyer" vous acceptez les conditions suivantes : Ne pas poster de message injurieux, obscène ou contraire à la loi, ni de liens vers de tels sites. Respecter la "netiquette", ne pas usurper le pseudo d'une autre personne, respecter les posts faits par les autres. L'auteur du site se réserve le droit de supprimer un ou plusieurs posts à tout moment. Merci !Ah oui : le bbcode et le html genre <br>, <a href=...>, <b>b etc. ne fonctionnent pas dans les commentaires. C'est voulu.