Voir aussi: mettre ici des notes entre [[]] vers des sujets voisins
What comes next Méthode de Newton(lien privé)

La découverte de l'intégrale de parité est due au regretté Gérard Langlet. Il écrivait ses programmes en APL, ce qui les rend difficile à comprendre.
Mais le principe est très simple :

il s'agit de la propagation de la différence (en APL : \#) appliquée à un vecteur binaire. La fonction intégrale de parité est l'inverse du Code Gray.

cf APL Langlet (Répertoire NAS)(lien privé)
facto/arithmetique et bits (Répertoire sur D)(lien privé)

et sur mon site :
factorisation Langlet code Gray. (page sur mon site)

Au moment ou il a fait cette découverte, Langlet s'intéressait au langage informatique APL. Ce nom ne vous dit peut-être rien, pourtant il s'agit d'un des premiers langages de programmation, presque aussi vieux que Cobol, Lisp, Basic, Fortran et PL/1. APL n'a pas eu le succès qu'il méritait, sans aucun doute parce qu'il nécessite un clavier spécial. En effet, ce langage, ultra puissant pour la construction de fonctions et d'expressions mathématiques, et en particulier le calcul matriciel, permet de définir tout fonction d'une manière extrêmement condensée, sous forme d'une chaîne de symboles ésotériques (APL est aussi réputé pour être illisible par les profanes) mais ultra-courte. Des fonctions qui nécessitent des pages de code C ou java (des langages "modernes") s'écrivent très souvent en APL sur une seule ligne !

En APL, l'opérateur binaire "#" signifie "différence". Ainsi 1#2 vaut 1 (1 est équivalent à "vrai" en APL), 1#1 vaut 0 parce que le 0 signifie aussi "faux" en APL (comme en Basic). Lorsqu'il est appliqué un un vecteur binaire (une chaîne de bits, valant chacun 0 ou 1), l'opérateur # est équivalent au XOR bit par bit des langages informatiques modernes (opérateur généralement noté "^" ). Ainsi 1 0 0 1 0#0 1 0 1 0(APL) = 18^10(Java) = = .

Mathématiquement, nous écrirons

En APL, le même opérateur a souvent un sens différent lorsqu'il a un ou deux arguments. Par exemple avec un seul argument qui est un vecteur de nombres, "#" signifie "faire les différences successives entre les nombres". Ainsi #2 3 4 vaut 1, parce que #2 3 vaut 1 (en effet 2 est différent de 3) et # 1 4 vaut 1 parce que 1 est différent de 4. Lorsque l'argument est une chaîne de bits, ou un nombre codé en binaire, # est l'opérateur (unaire ou binaire) parité : #100110 vaut 1 parce que le nombre de bits "1" est impair.

Gérard Langlet s'intéressait à l'opérateur APL de balayage, noté "" en APL : cet opérateur unaire prend en argument une fonction à deux arguments, et applique cette fonction entre tous les nombres d'un vecteur. Ainsi en APL "+1 2 3 4" renvoie la valeur 10, somme des quatre nombres 1, 2, 3, et 4. De même "* 1 2 3 4" renvoie la valeur 24, produit de ces quatre nombres.

Langlet a donc essayé de trouver les propriétés de l'opérateur suivant : \#. Cette fonction s'interprète ainsi : "Balayer successivement tous les bits du nombre et appliquer l'opérateur # entre chaque bit et le résultat obtenu pour le bit précédent".

Langlet l'a appelé propagation de la parité", ou encore intégrale de parité, pour des raisons que nous n'expliquerons pas ici. Par exemple #\1010 effectue les opérations suivantes :

En langage mathématiques, et parce que APL est (quand même) un peut démodé 😉 nous noterons L'opérateur de propagation de parité : donc

Langlet s'est alors demandé ce qui se passait en itérant à nouveau la propagation de la parité sur ce résultat, et ainsi de suite. On obtient une séquence cyclique de nombres (on revient toujours sur le nombre de départ), que Langlet a appelé le Pariton du nombre de départ.

Ainsi, en partant de "10110011", on obtient :

#TBC calcul faux (gray)
la suite est périodique. Si l'on part d'un nombre N, dont le nombre "1" est m (on l'appelle la masse du nombre N), alors la taille du cycle est la première puissance de 2 supérieure ou égale à m.

Dans l'exemple, ci-dessus m=5 et la période est 8.

en partant de "111111", on obtient :

cf le calculateur excel : pariton.xls (Fichier sur D)(lien privé)
#TBC calcul faux

Les paritons issus des séquences 111... sont appelés Génitons . En partant de d'un nombre de bits "1" en nombre , on obtient le géniton d'ordre , noté

De telles structures sont récursives et même fractales : les seize nombres situés dans le coin supérieur gauche du géniton-8  constituent précisément  le géniton-4. En fait le géniton d'ordre 8 est précisément composé de :
G4 G4
G4 Z4
où Z4 est la matrice 4x4 remplie uniquement de zéros.
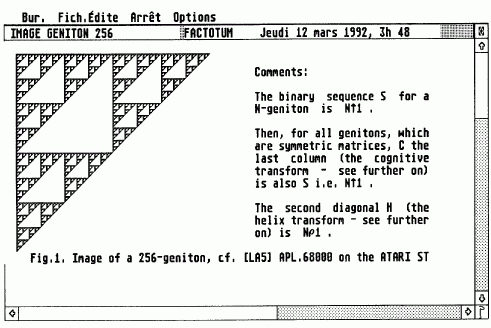
Voici une image du géniton G(256)

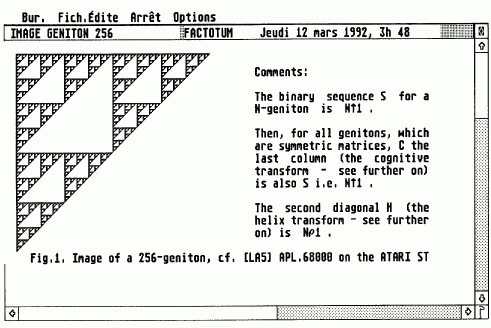
On remarque qu'il s'agit d'une structure en tapis de Sierpinski, bien connu des matheux parce qu'il s'agit de la représentation de la parité des nombres dans un triangle de Pascal.

On peut également disposer les différences en triangle, ce que Langlet appelait le fanion :

Ce qui fait penser au triangle de Pascal et au What comes next Méthode de Newton(lien privé)

Langlet appelle "signal binaire" le sommet de ce triangle, et Hélicon le coté gauche, 1101111001 . Il nommait aussi Cogniton le coté droit, lu de bas en haut : 11100110100

On peut aussi les retrouver à partir du pariton de B :

Langlet a découvert les relations suivantes :

La suite sur le site factorisation Langlet code Gray. (page sur mon site)

et Mes recherches mathématiques