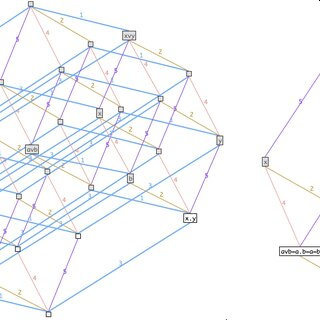Le problème de la satisfiabilité d'une expression logique est le problème NP-complet le plus connu et le plus étudié.

J'ai cherché des solutions polynomiales à SAT, ce qui prouverait P=NP, Un de mes rêves...(lien privé)

J'ai choisi de travailler sur le problème SAT-3 en forme normale conjonctive (CNF)

J'ai essayé un grand nombre d'algorithmes :
cf. SAT (Répertoire sur D)(lien privé), ou SAT (Répertoire NAS)(lien privé)

Mais finalement j'ai retenu une analogie "électrique" à ce problème :

Dans le doc « SAT et logiques multi valuées », j’avais proposé une analogie électrique à la forme CNF d’un problème SAT-3 : par exemple 

(v1 | ~v2 | ~v3 ) & (~v1 | ~v2 | v4 ) & (v2 | v3 | ~v4 ) & (~v1 |  v2 | v4 )

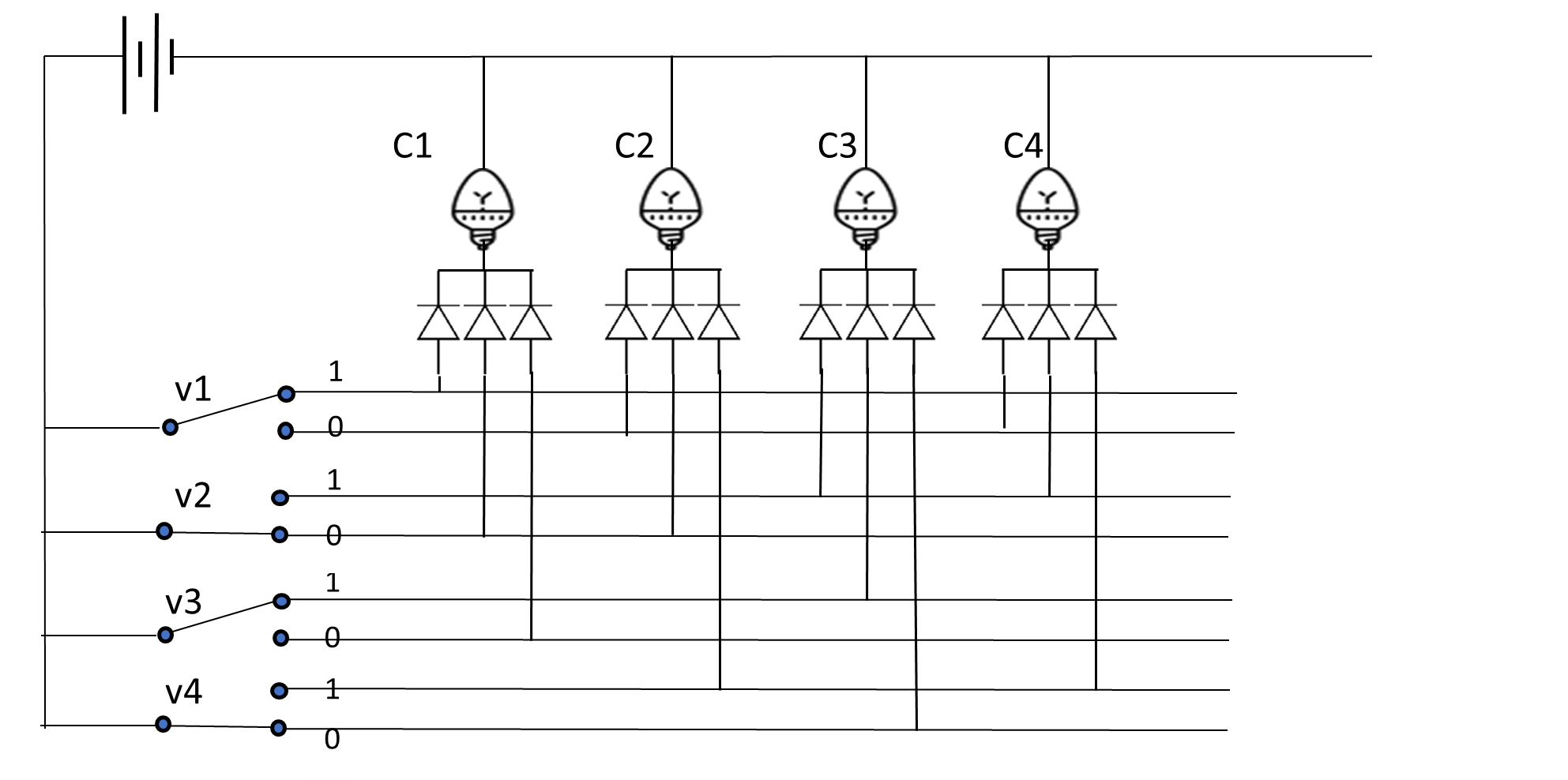
Les triplets de diodes que l’on voit sous les ampoules agissent comme des « ou » : la lampe est allumée des que le courant traverse au moins une diode. Chacun des littéraux d'une clause correspond à une diode reliée à une ligne. On voit que pour chaque variable il y a deux lignes horizontales, l’une correspondant au 0 (faux) et l’autre au 1 (vrai).

Dans le cas de cet exemple, il n'y a que 4 variables et il suffit donc d'énumérer les 16 possibilités :

Ici, ce n’est pas le cas car C4 n’est pas satisfaite. Mais on voit rapidement qu’il suffit d’inverser la position de l’interrupteur v4 pour que cela marche. Mais en fait les solutions sont :
(v1,...,v4) = (0 0 0 0 ), (0 0 1 0), (0 0 1 1 ), (0,1,0,0), (0 1 0 1) , (1 0 1 1 ), (1 1 0 1 ), (1 1 1 1)

La "traduction" d'un problème 3-SAT posé sous forme CNF en analogie électrique est triviale.

Cette analogie m’avait conduit à proposer quelques algorithmes qui malheureusement n’ont pas fonctionné aussi bien que je l’espérais : la solution est bien trouvée, mais en temps exponentiel.

Si V est le nombre de variables, le nombre de configurations possible est bien sûr

Généralement dans les problèmes concrets, le nombre de clauses est largement supérieur au nombre de variables (C>>V)

Je propose aujourd’hui de renverser, en quelque sorte, le sens du courant, comme ceci :

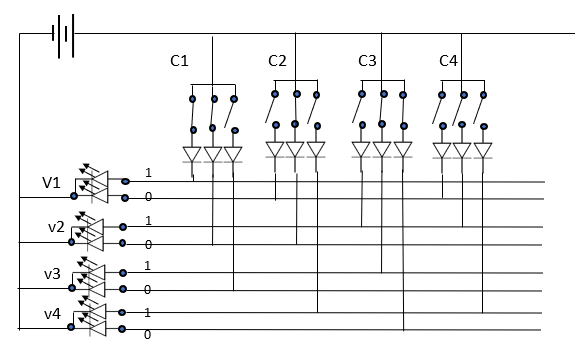
J'appelle ce montage une "configuration SAT3 duale".
Chaque clause est associée à un triplet d'interrupteurs.

Chaque littéral d'une clause correspond à un interrupteur alimentant une diode (verticale) reliée à une ligne (horizontale); cette ligne conduit à une LED verte pour un littéral positif, rouge pour un littéral négatif.

Les variables sont donc ici des LEDs bicolores (rouge +vert). On a donc 4 états possibles :

Si nous avons une solution au problème SAT, cela signifie que nous avons déterminé l'état T ou F de toute les variables, et donc il existe une configuration des interrupteurs telle que au moins un des interrupteurs de chaque clause est fermé et aucune diode ne sera dans l'état jaune.

Mais en fait pour satisfaire une clause il suffit que un et un seul de ses trois littéraux soit satisfait. Donc on peut simplifier le montage ainsi :

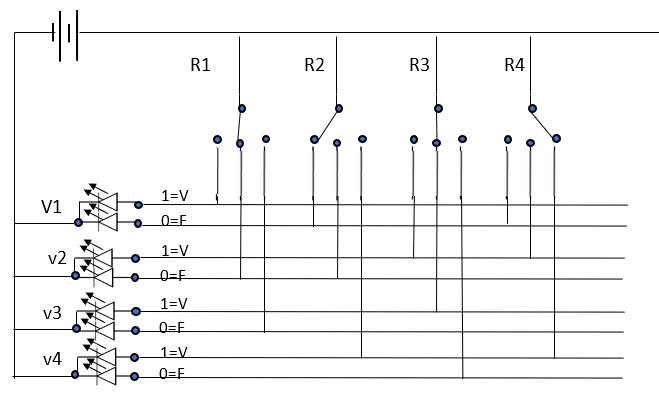
J'appelle ce montage une "configuration SAT3 duale réduite".
Chaque clause est associée à un des "rotacteurs" R1..R4.

Chaque rotacteur choisit donc, pour chaque clause, un seul littéral qu'il faut satisfaire (ce qui satisfera la clause). L’état de l’ensemble de tous les rotacteurs peut être représenté par un nombre en base 3, ainsi pour la figure 3 ce sera 1012₃

On dira que le rotacteur R pointe vers la ligne i s'il alimente effectivement cette ligne, et de même pour la diode à laquelle appartient cette ligne. Par exemple dans la fig 3, R1 pointe vers la ligne et la diode associée à la variable

Soit donc le problème P suivant :

Par exemple, la configuration des rotacteurs (1,2,2,3) donne la configuration des diodes (vert,rouge,vert,vert) et donc les variables (1,0,1,1) qui est une solution.
Inversement, la configuration des rotacteurs (1,1,1,1) donne la configuration des diodes (jaune,vert,noir,noir), et donc il est impossible de déterminer la variable v1.

Le nombre de configurations possibles ne dépend plus du nombre de variables, mais du nombre de clauses C; il est évidemment de . Comme généralement dans les problèmes réels , le problème semble donc plus compliqué encore que le problème 3-SAT. Pourtant on a le théorème :

Soit S une configuration des rotacteurs (cf Fig 3); Si S est une solution du problème P, Les diodes sont donc dans l'état noir, vert ou rouge. Chaque rotacteur R alimente donc une unique ligne L appartenant à une variable (et donc une diode) V. l'autre ligne L' de V est forcément à l'état zéro, sinon la diode serait jaune. On peut donc en déduire l'état (0 ou 1) de chaque ligne horizontale. Pour les diodes noires, on peut choisir arbitrairement de mettre l'interrupteur en position 0 ou 1.

On "renverse" alors le courant pour passer de la Fig 3 à la Fig 1. et on alimente les lignes avec les interrupteurs en position 0 ou 1 correspondants. Toutes les lampes des clauses sont alors allumées et on a donc une solution du problème SAT-3.

Si le problème P n'a pas de solution, c'est que quelle que soit la configuration des rotacteurs, l'une des LED sera alors jaune (pas forcément la même). A fortiori si l'on remplace les rotacteurs de la fig 3 par les interrupteurs de la fig 2. Donc quelque soit la position des interrupteurs, il n'est pas possible de trouver une configuration sans diode jaune. En inversant le sens du courant pour passer à la fig 1, aucune configuration des variables ne peut alimenter (satisfaire) toutes les clauses.

L'idée est de choisir une position tout à tour pour chaque rotacteur de la fig 3, en tenant compte du fait que si on choisit pour un rotacteur r une position qui pointe vers une variable (ou ligne) v, on peut supprimer les positions des autres rotacteurs qui pointent vers cette même variable avec un signe opposé (puisque cela ne servirait qu'à mettre la LED en jaune), et carrément supprimer de la recherche les autres rotacteurs dont une position pointe vers v avec le même signe, puisqu'il suffira de les positionner vers v pour les satisfaire.

Si pour une clause (v1 | v2 | v3) on choisit une position correspondant au littéral +v1, alors on supprime toutes les autres clauses avec +v1 et, toutes les positions -v1 dans les les autres clauses (ce qui peut forcer l'état d'autres variables). En outre les variables v2 et v3 deviennent moins contraintes.

On peut simplifier le problème 3-SAT, comme suit : (ce qui est une phase d'initialisation avant l'algorithme proprement dit)

Répéter tant qu'une des actions ci dessous est possible :

A l'issue de cette phase, chaque clause contient deux ou trois littéraux, une variable ne peut apparaitre qu'une seule fois dans une clause, et chaque variable apparait au moins dans deux clauses.

Souvenons-nous que le but final est de supprimer les LED jaunes !

Imaginons un problème avec 1000 clauses, donc 1000 rotacteurs et 3000 positions possibles. On peut essayer de supprimer des positions possible et de faire faire les choix les plus informant, mais cela conduit à un algorithme exponentiel

On notera :

On a bien sûr :

puisque chaque rotacteur alimente une ligne, mais que plusieurs rotacteurs peuvent alimenter la même ligne.

Notons que dans une solution, toutes les diodes sont vertes ou rouges ou noires (). Dans une solution,

Enfin, on notera, pour une configuration donnée des rotacteurs :

Bien sûr pour une diode donnée son état dépend de son statut :

On notera que la diode n'est pas jaune.

Enfin puisque chaque rotacteur pointe vers une seule ligne, le statut de la diode associée à cette ligne est aussi le statut du rotacteur et donc de la clause.

Un mouvement correspondra au changement de position d'un rotacteur de la position à la position , avec

Supposons qu'un rotacteur R pointe à un moment donné vers une ligne de signe , qui alimente une diode , et on a donc avec

Après un mouvement de R, le nouveau score de sera , et donc il aura diminué de (qui peut être éventuellement nul).

Remarque : le score initial de est aussi le score initial du rotacteur , mais également celui de tous les autres rotacteurs qui pointent vers .

Mais dans sa nouvelle position le rotacteur pointera vers une diode (forcément différente, , cf. simplification ci dessus), via une ligne de signe .

Si le score de était , Après le mouvement, il sera , et donc il aura augmenté de (qui peut être éventuellement nul)

Au final le score heuristique du problème aura varié de

L'autre effet du mouvement est que (sans la barre) a été décrémenté de 1 et a été incrémenté de 1.

Le problème consiste donc, à partir d'une configuration arbitraire des rotacteurs, dont la somme heuristique est , à trouver un ensemble de mouvements qui réduisent S à 0.

On peut utiliser certaines variables :

Nous utiliserons ici seulement S

Si nous considérons la fonction qui associe à chaque mouvement la variation du score due à , c'est à dire , alors

Si est le mouvement nul, si " " dénote le mouvement A suivi du mouvement B, si est le mouvement opposé de , donc , et nous avons :

En effet tant que des mouvements successifs A et B mettent en jeu des rotacteurs différents, l'ordre de ces mouvements est sans importance : les rotacteurs se retrouveront au final dans la même position, donc la variation du score final sera la même et elle sera la somme des deux variations dues à chacun des rotacteurs.

Pour un même rotacteur , si l'on veut pouvoir effectuer dans l'ordre aussi bien les mouvements que , la seule possibilité est le mouvement nul :

On remarque que la fonction possède les mêmes propriétés que le logarithme...

#TBC

Lorsqu'on bouge un rotacteur qui pointe vers la ligne d'une diode jaune , le but est bien de contribuer à supprimer la lumière jaune. Pourquoi alors ne pas alors bouger tous les rotacteurs qui pointent vers ? On éteindrait alors la ligne .

On a alors deux choix de destination pour chacun de ces rotacteurs . L'idée est de choisir pour chacun la position qui minimise , l'augmentation de due au mouvement de

Donc :

Est-ce que le processus converge ?
Et si le problème n'a pas de solution ?
Complexité ?

Un autre algo, tout bête : choisir à chaque étape un mouvement qui fasse décroitre le score S.

Si c'est le cas et si a valeur dans , alors au départ elle doit valoir au moins le nombre de mouvements à effectuer...

#TBC

J'ai eu une idée complètement différente : au lieu de chercher un algorithme, considérons le problème SAT comme un jeu à somme nulle. Les deux joueurs sont "Vérifieur" et "Falsifieur". Vérifieur cherche à satisfaire l'équation, c'est à dire à trouver une assignation des variables qui rendent l'équation vraie (ou une position des rotacteurs qui éteigne les diodes jaunes), falsifieur tente de prouver que ce sera impossible.

La version la plus simple d'un jeu basé sur 3-SAT est la suivante :

Deux joueurs (MAX et MIN) jouent sur une instance SAT en assignant alternativement une valeur de leur choix, vraie ou fausse, à une variable non utilisée. MAX gagne si et seulement si la formule est vraie après que toutes les variables ont été affectées.

Mais on peut aussi considérer que le jeu se déroule sur un graphe coloré où les nœuds représentent les clauses et les variables, et où chaque arc relie une clause à une variable :

On a C boîtes (1 par clause) contenant chacune 1 à 3 jetons colorés. Il y a V couleurs possibles (une par variable) et les jetons sont soit carrés (littéral positif) soit ronds (littéral négatif).

Dans ce jeu il y a un seul joueur (c'est un solitaire)

Un tour de jeu consiste à retirer un ou plusieurs jetons. Il sera gagné si à la fin tous les jetons d'une couleur donné ont la même forme, et si chaque boîte contient au moins un jeton.

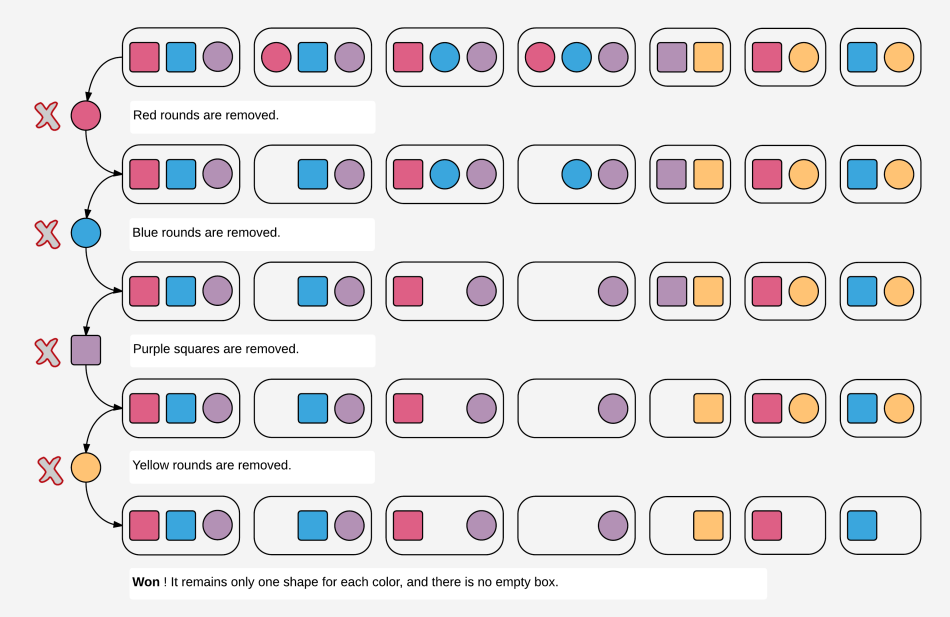
Plusieurs variantes sont possibles pour définir les coups légaux. Par exemple pour la variante "Un coup consiste à retirer tous les jetons d'une même forme et couleur", on pourrait avoir la séquence de coups suivantes pour un problème donné (ici avec 7 clauses et 4 couleurs) :

Ce jeu a été décrit (mais pas vraiment analysé) dans https://arxiv.org/pdf/1511.00813

Une variante intéressante est : "Un coup consiste à retirer un jeton quelconque d'une boite quelconque, mais en s'assurant qu'aucune boîte n'est vide". Le jeu se termine lorsque chaque boîte contient exactement un jeton. Le joueur gagne si et seulement si tous les jetons d'une même couleur ont la même forme.

On notera la ressemblance, et même l'équivalence, de cette variante avec Un autre jeu Couper les arcs

On dispose d'un tas de jetons en forme de triangles. Leurs coins portent chacun un numéro et une couleur : bleu ou rouge

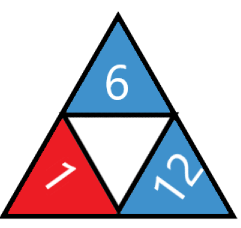
Deux jetons différents peuvent avoir un ou même plusieurs numéros en commun, avec ou pas les mêmes couleurs. Mais sur un jeton donné, tous les numéros doivent être différents. Le tas de jeton constitue "le problème".

En outre il y a un tapis de jeu gravé d'une série de "colonnes" (1 par variable) en ligne, portant chacune un numéro (en ordre croissant) de 1 à n, et deux "places" respectivement bleue et rouge

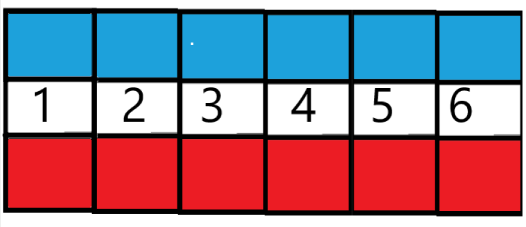
En général il y a plus de jetons que de colonnes sur le tapis. (C>V)

Le but est de poser tous les jetons un à un sur ces places en respectant les deux règles :

L'analogie avec SAT est évidente. Le problème est représenté par l'ensemble des jetons en triangles (un triangle par clause). Le signe des littéraux correspond aux couleurs. Poser un triangle sur une place p de couleur c signifie que l'on positionne la variable p à la valeur (Vrai, Faux) associée par convention à la couleur c, et donc que la clause est satisfaite par cette variable.

Un tour de jeu consiste soit à prendre un jeton triangulaire dans le tas et à le poser sur une place (vide ou déjà occupée, peu importe) en respectant les règles ci-dessus, soit à déplacer un triangle de la place où il se trouve vers une autre place "légale" pour ce jeton. Mais il y a une règle supplémentaire :

Avec deux joueurs, qui gagne ? Le gagnant est celui qui pose le dernier jeton (le C-ième), ou bien qui force son adversaire à se trouver dans une configuration où il n'a plus de coup légal.

On notera que si le problème est satisfiable, poser le dernier jeton donne une solution. S'il ne l'est pas, le jeu s'arrêtera une fois que toutes les configuration ont été explorées, ce qui peut prendre un certain temps, et même un temps certain 😉

Un tour de jeu consiste dans cette variante à prendre un jeton dans le tas et à le poser sur une place "légale". La différence avec la première variante est qu'il est impossible de déplacer le jeton une fois posé. Le jeu dure donc au plus tours.

On notera la ressemblance avec le jeu de Hackenbush qui a été analysé par Conway dans Winning ways. cf théorie des jeux(lien privé)

On dispose de deux ensembles de points, arrangés sur deux lignes horizontales : la ligne des clauses et la ligne des variables. Deux ou (généralement) trois arcs partent de chaque point de la ligne des clauses vers un point de la ligne des variables, et chaque point de la ligne des variable reçoit au moins un arc. Ces arcs peuvent être bleu ou rouge (bleu pour un littéral positif, rouge pour un littéral négatif) :
ici
C1=(v1 | ~v2 | ~v3 )
C2=(~v1 | v2 | v4 )
C3=(v2 | v3 | ~v4 )
C4=(~v1 |  ~v2 | v4 )

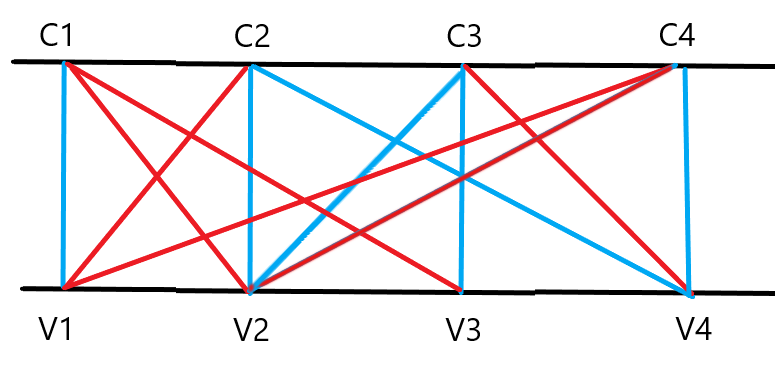
Le jeu consiste à couper successivement des arcs, de manière à ce qu'à la fin la condition suivante soit respectée :

Ici encore on a une analogie avec le jeu de Hackenbush, et l'analogie avec SAT est évidente : Une fois que la condition de fin est respectée, on a une solution : de chaque clause part un arc qui la rend vraie.

Dans l'exemple ci-dessus, il existe de multiples solutions, par exemple il suffit de couper tous les arcs bleus, ou tous les arcs rouge. C'est parce que le problème est très simple et que le nombre de clauses n'est pas très grand. Bien sûr ce n'est pas toujours possible dans le cas général...

Si le problème SAT n'a pas de solution, aucune suite de coups (ou de coupes !) ne peut arriver sur une position qui respecte la condition de fin.

Plusieurs règles de jeu sont possibles pour déterminer qui gagne et qui perd et quand :

On peut imaginer deux joueurs, bleu et rouge, qui jouent tour à tour.
Un tour de jeu consiste donc à couper un des arcs, en respectant les règles suivantes :

Le jeu s'arrête lorsqu'un joueur n'a pas de coup possible, et le joueur qui a le trait est le perdant, sauf si à ce moment une variable quelconque porte des arcs de plusieurs couleurs, et ce joueur est alors gagnant. #TBC (? A REVOIR)

Un joueur, bleu ou rouge, ne peut couper que certains arcs :

Le jeu s'arrête de la même façon que pour la variante 1.

Au départ il y a 3C arcs, trois partants de chaque clause. A chaque coup le joueur qui a le trait coupe un arc (de n'importe quelle couleur), mais en s'assurant que chaque clause a toujours au moins un arc. Le jeu dure donc exactement 2C coups et à la fin, c'est donc le joueur 2 qui coupe le dernier arc, et chaque clause possède exactement un arc.
Si à ce moment chaque variable n'a que des arcs de la même couleur, le dernier joueur (donc le second) perd, sinon il gagne.
On remarque que si le dernier joueur perd, le problème SAT est résolu avec succès.

On associe à chaque variable le i-ième nombre premier . Un littéral sera défini par si le littéral est positif, et si le littéral est négatif. Une clause formée de trois littéraux sera représentée par le produit . A partir du nombre rationnel , il est possible par factorisation de déterminer les littéraux de la clause.

Par exemple la clause C1=(v1 | ~v2 | ~v3 ) sera représentée par (ou aura la valeur)

Si la clause contient deux (ou trois) fois la même variable avec le même signe, on ignorera l'exposant résultat. par exemple la clause C1=(v1 | v1| ~v3 ) aura la valeur et non

Si la clause contient une même variable avec des signes opposés, la valeur de la clause sera nulle par convention. (La clause sera toujours vraie)

Si l'on considère le produit des valeurs de deux clauses, on constate que les littéraux de signe opposés se simplifient, et que l'exposant du nombre premier associé à deux littéraux de même variable et même signe augmente.

Par exemple le produit des valeurs des deux clauses  C1=(v1 | ~v2 | ~v3 ) et  C2=(v1 | v2 | v4 ) sera

On appellera problème la l produit des valeurs, ainsi définies, de clauses. ???

Il est clair que si deux clauses partagent une même variable ,

#TBC

cf créneaux et briques

En fait l'arbre des valeurs possibles des variables peut se représenter par des cercles concentriques, autant que de variables :

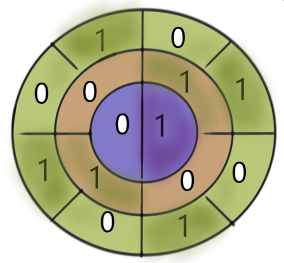
La variable v1 en violet au centre, avec ses deux valeurs possibles, puis v2 en orange, V3 en vert, etc. Ainsi chaque assignation comme (0,0,0,...) correspond à un secteur angulaire.

On peut bien sûr avoir aussi une représentation en tableau :

Chaque clause du problème va restreindre les secteurs possibles (et donc les variables)

Par exemple avec 4 variables et toujours
C1=(v1 | ~v2 | ~v3 )
C2=(~v1 | v2 | v4 )
C3=(v2 | v3 | ~v4 )
C4=(~v1 | ~v2 | v4 )

pour C1=(v1 | ~v2 | ~v3 ) , les valeurs ou secteurs angulaires (0,1,1,?) sont interdites dans une solution. De même avec C2= (~v1 | v2 | v4 ) --> secteurs (1,0,?,0) interdits :

Les X marquent les secteurs interdits. Tant qu'il reste des trous (crénaux), donc des zéros dans le mot binaire ALL, le problème est solvable.

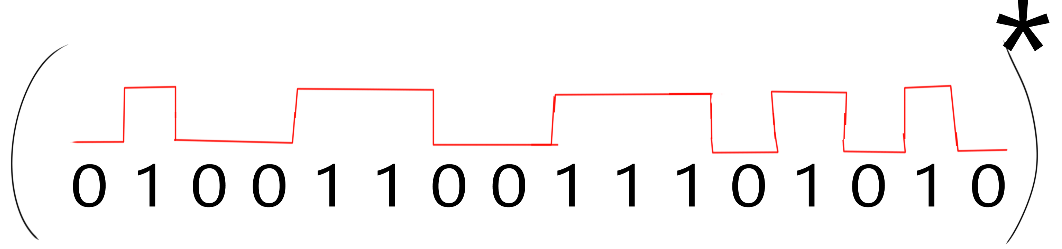
Inconvénient de cette solution, il faut un tableau à éléments ce qui est rédhibitoire... Mais on peut compresser ce tableau.
Par exemple la solution trouvée, 0100001011101010
se compresse en
cf répétitions dans une séquence > autre algorithme de compression de chaînes de symboles (plus rapide !)

Mais il est possible de faire mieux. cf créneaux et briques. Une variable est une brique. Un littéral est une brique ou sa négation. Une clause est le OR de trois briques littérales, comme suit :

Donc un algorithme possible est de prendre en compte les clauses une à une, et à maintenir la liste (compressée) des solutions restantes sous forme d'une chaîne de bits. Inconvénient, pour un problème à 10000 clauses, cette liste non compressée ferait bits de long... Mais on peut s'arranger : il suffit de garder la position de la première solution supérieure à une certaine constante (initialement 0), et de tout recommencer en augmentant la constante si la solution est finalement invalidée par l'ajout d'une clause.

Notons que tous les littéraux positifs correspondent à des créneaux de la forme et les littéraux négatifs à , où est le numéro de la variable (en commençant par ) (Les "1" dans ces créneaux représentent les valeurs possibles)
Le OU de deux littéraux positifs et (q>p) correspond donc à
Le OU de trois littéraux a l'allure suivante : (ici pour v1,v3,v5) :

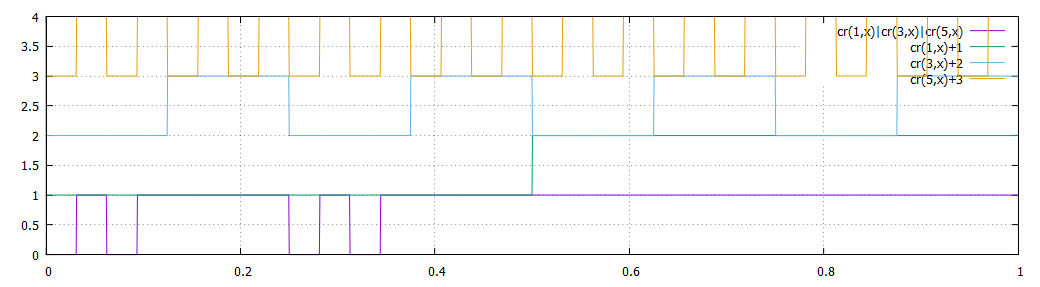
code gnuplot : (n>0 pour un littéral positif, < 0 sinon)

et donc le graphe de notre problème du début :

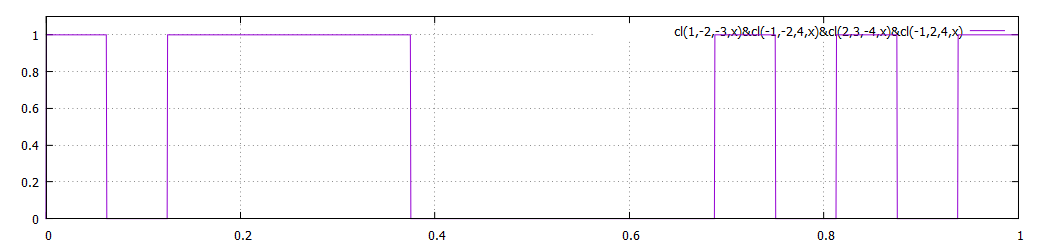
cf aussi en python : (cliquer sur RUN)

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 1, 300)
# créneau (variable)
def cr(n,x):
	return np.mod(np.floor(x*2**n),2)
# littéraux
def li(n,x):
	if n>0:
		return cr(n,x)>0
	return (1-cr(-n,x))>0
# clause
def cl(a,b,c,x):
	return li(a,x)|li(b,x)|li(c,x)

plt.figure(figsize=(8,2)) #inches

#plt.plot(x,li(2,x))
#plt.plot(x,cl(2,3,-4,x))
plt.plot(x, cl(1,-2,-3,x)&cl(-1,-2,4,x)&cl(2,3,-4,x)&cl(-1,2,4,x))
plt.show()
Run

plt.figure(figsize=(8,2)) #inches
plt.plot(x, cl(1,-2,-3,x))
plt.show()
Run

L'idée ici est de trouver une fonction suivant(n,x0) qui donne l'abscisse du prochain x1 supérieur à x0 pour lequel on a un résultat "1" pour la conjonction de toutes les clauses de numéro inférieur ou égal à n, ou "impossible" s'il n'y en a pas . l'abcisse en question est 0."le nombre binaire qui décrit la valeur de toutes les variables".

l'algorithme pour SAT est alors le suivant (C est le nombre de clauses)

Pour accélérer l'algo, on va utiliser le fait que l'on peut classer les clauses avant l'éxécution.

La partie compliquée est bien sûr la fonction suivant() ; Mais les 3-clauses n'ont que 8 formes possibles, #TBC

Si on considère un sous-ensemble des clauses du problème (par exemple a première moitié), on peut déterminer quels arcs et variables sont liées à ainsi que les arcs "sortant" des clauses de E vers des variables de , et les arcs reliant les variables de aux clauses de

On peut alors résoudre le sous-problème pour une valeur donnée du vecteur , ce qui impose une valeur à ...

#TBC

l'idée est de s'inspirer de la solution quantique au problème du carré gréco-latin d'ordre 6, trouvée en 2022... cf Le problème des 36 officiers (page web sur le site de Pour la Science)

Les données utilisées sont :

On utilisera une fonction utilitaire etat-diode(d) Qui donne l'état de la LED double avec . Il y a une diode double par variable. A chaque LED double correspond un couple de deux lignes, celle à l'indice et celle à l'indice . Inversement, à chaque ligne correspond une diode, à l'index . Par conséquent, chaque diode peut être dans l'un des quatre états ''noir", "rouge", "vert", "jaune", ou encore (0,0),(0,1),(1,0),(1,1). :

Ou bien tout simplement une fonction diode_ok(d) qui renverrait FALSE dans le cas doublement pointé.

Après simplification ( cf supra) :
Initialiser C et V, et la table T (en tenant compte des simplifications)
Remplir la liste des rotacteurs R en les positionnant tous à la position 1 et avec l'ensemble de positions {1,2,3}, sauf pour les clauses qui n'ont que deux littéraux où ce sera
Initialiser la liste des lignes à l'état "non pointé"
Utiliser la table T pour trouver, pour chaque rotacteur, la ligne pointée et la positionner à "pointé"
si état_diode(d) n'est "jaune" pour aucun d,
retourner SUCCES. (coup de chance !)

On peut imaginer plusieurs algorithmes :

La fonction trouver_solution(i) cherche s'il existe une solution pour les clauses (rotacteurs) i à C inclus.
La fonction retourne SUCCES ou ECHEC.
Elle utilise les listes L et R et peut les modifier (pour les index entre i et C), néanmoins au retour en cas d'ECHEC elle doit les rendre dans l'état où elle les a trouvé en entrant. Dans le cas SUCCES, la liste R contient au retour les positions de tous les rotacteurs de 0 à C, et la liste L les états de toutes les lignes de 0 à 2V
L'algorithme se lance donc par trouver solution(1)

#TBC

Supposons un problème SAT-3 avec V variables, C clauses et au maximum 3 littéraux par clause. On va créer un tableau (matrice) à C lignes et V colonnes. La case (c, v) = vaudra 0 si la variable v n'est pas dans la clause c, et ±1 sinon, selon le signe du littéral de la variable dans la clause .

(on supposera, sans perte de généralité, que la même variable ne peut figurer deux fois dans une même clause, et que toutes les clauses contiennent exactement 3 variables distinctes cf Simplification initiale)

Par exemple pour :
C1=(v1 | ~v2 | ~v3 )
C2=(~v1 | v2 | v4 )
C3=(v2 | v3 | ~v4 )
C4=(~v1 | ~v2 | v4)
C5=(~v1 | ~v3 | ~v4)

La matrice sera :

Assigner une valeur (T,F) à une variable, c'est inverser (F) ou pas (T) la colonne correspondante de la matrice. Une clause est satisfaite si la ligne correspondante contient au moins un "1" une fois que toutes les variables sont été assignées. (Dans l'exemple, la clause C5 n'est pas satisfaite initialement mais il suffit d'inverser v1 ou v3 (ou les deux !), c'est à dire de leur donner la valeur "faux" pour trouver une solution)

En fait l'instance de départ (avec toutes les variables égales à T) n'est pas satisfiable si et seulement si une ligne de la matrice a une somme égale à -3, puisque il y a exactement 3 variables par clause. Cela sera vrai également pour toute instance obtenue en donnant aux variables une valuation booléenne quelconque.

Notons que comme il y a 3 variables non nulles par clause, la somme d'une ligne de la matrice vaut forcément -3, -2,-1, +1, +2 ou +3.

Le vecteur somme ligne vaut , où est le vecteur colonne constitué de "1".
Si nous ajoutons 3 à chaque élément de ce vecteur , le problème SAT est satisfiable si et seulement si le produit des éléments du vecteur résultat est non nul.
nb: on pourrait aussi à la place ajouter 1/V à chaque élément de

Le problème général de satisfiabilité consiste donc à trouver un vecteur de représentant les assignations (F ou T) à donner aux variables.
A partir de , on crée une matrice carrée diagonale par , puis un vecteur colonne
Si le produit des éléments de est différent de 0, le problème SAT est résolu.

La somme d'une colonne, elle, peut varier entre -V+1 et +V-1, où V est le nombre de variables, en effet chaque colonne contient au moins un +1 et un -1, en effet s'il y a un +1 il y a aussi un -1 et réciproquement, sinon tous les littéraux de cette variable auraient le même signe et on l'aurait retirée du problème dans la phase d'initialisation.

Notons qu'on crée un problème dual en transposant la matrice :
C'1 = ( v'1 | ~v'2 | ~v4 | ~v5')
C'2 = (v'2 | v'2 | v'3 | ~v'4)
C'3 = (v'1 | v'3 | ~v'5)
C'4 = (v'2 | ~v'3 | v'4 | ~v'5)
et que bien sûr et sont des matrices carrées symétriques, de déterminants respectifs 0 et 65 :

cf Python > matrices et python
Que deviennent ces produits si on inverse une variable ?
#TBC

Mes recherches mathématiques