Journal d'un Terrien

Web log de Serge Boisse

On line depuis 1992 !

Si cette page vous a plu, Copiez son adresse et partagez-la !
http://sboisse.free.fr/science/maths/Mes Recherches mathematiques/factorisation/factorisation par insertion de bits.php

Savez-vous quels sont les articles les plus vendus sur Amazon.fr ?

Bricolage Hygiène santé Mode Beauté Maison Sport et loisirs Livres Gadgets

factorisation par insertion de bits

science > maths > Mes Recherches mathématiques > factorisation > factorisation par insertion de bits

Factorisation par insertion de bits

Résumé : recherche d'un algorithme de factorisation rapide.

Attention

Ceci est une recherche en cours. Elle n'est pas encore terminée. Cette page est susceptible d'évoluer dans le futur...

cf facto par insertion de zeros (Fichier sur D)(lien privé) (lien privé)

notations

Dans ce qui suit, sont des entier positifs ou nuls ;
seront soit des entiers soit des réels suivant le contexte.
On utilisera parfois la typographie Latex, comme soit une typographie plus orienté "code informatique" comme x**2.

On notera a^b ou le XOR bit à bit de et (comme dans les langages informatiques C, javascript, etc.)
a^a=0

On notera ** la fonction puissance : 2**3=8 ou en Latex
On notera % la fonction modulo : = 13%4 = 1

on notera aussi g(n) le code Gray de n : g(n)=n^(n/2) où n/2 = n>>1 c'est à dire le décalage des bits de n de 1 cran à droite sans virgule. Par exemple g(554)=831.
On peut démontrer que

g(a^b) = g(a)^g(b)

L'inverse de cette fonction g est l'intégrale de parité chère à Gérard Langlet qui en a fait l'analyse exhaustive. Si nous appelons ig cette fonction réciproque de g, on peut la calculer ainsi :

ig(x) = ig2(0,floor(x))
ig2(r,n) = (n<=0) ? r: ig2(r^n, n/2)

Et on a n= g(ig(n)) = ig(g(n)) et ig(a^b) = ig(a)^ig(b)

Le mélange par insertion de bits

Dans ce qui suit a,b,c,d,n,m sont des entiers positifs. On note a\b ou le mélange par insertion des bits de a et b (qui se termine par ... )
Par exemple

123 =    1 1 1 1 0 1 1
25  =     0 0 1 1 0 0 1
123\25 = 10101111001011 = 11211 en base 10

a\b avec gnuplot :
ins(a,b) = (a==0&&b==0)?0:(b&1)+2*(a&1)+4*ins(a/2,b/2)

fonctions pairs et impairs

Notons que si pairs(a) et impairs(a) représente respectivement les nombres obtenus par la concaténation des bits pairs et impairs de a (le bit de poids faible est selon la convention informatique usuelle le bit 0, c'est à dire pair), alors pour tout entier a, a= impairs(a)\pairs(a)

On définit ainsi les fonctions pairs et impairs :
pairs(b)= (b<=0)?0:(b%2)+pairs(b/4)*2
impairs(a)= (a<=1)?0:((a/2)%2)+impairs(a/4)*2
Par exemple pairs(11)=1, impairs(11)=3 parce que

On remarquera que pour tout , a = 0\pairs(a)+ impairs(a)\0

pairs(n)=0 pour n = 0, 2, 8,10,32,34,40,42,128,130 = A062880 c'est à dire les nombres de la forme k\0
pairs(n)=1 pour n = 1,3,9,11,33,35,41,43,129,131 qui est la suite précédente +1
impairs(n)=0 pour n = 0, 1, 4, 5, 16, 17, 20, 21, 64, 65, 68, 69, 80, 81, 84, 85 ... = A000695 c'est à dire les nombres de la forme 0\k
impairs(n)=1 pour n = 2,3,6,7,18,19,22,23,66,67,70,71,82 ... qui est la suite précédente +2

)

et l'encadrement :
pairs(x) <= 2**(floor(log2(x))/2+1)-1
pairs(x)> >= (2**(floor(log2(x))/2))* ((floor(log2(x))+1)%2)

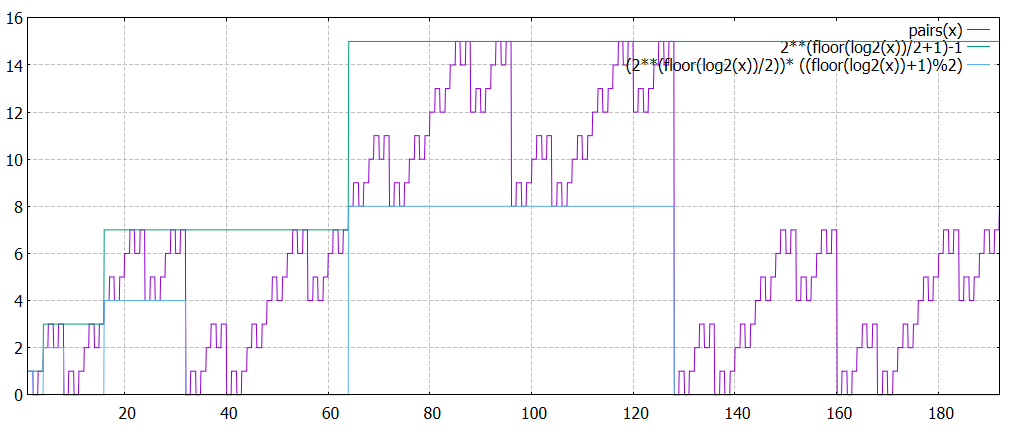
Pasted image 20240822222631.png

ppi(x) = pairs(x)+impairs(x)

si on pose ,
prend les valeurs 1,1,2,2,3,3,4,2,3,3,4,4,5,5,6,4,5,5,6,6,7,7,8,6,7,7,8,8,9,9
En fait

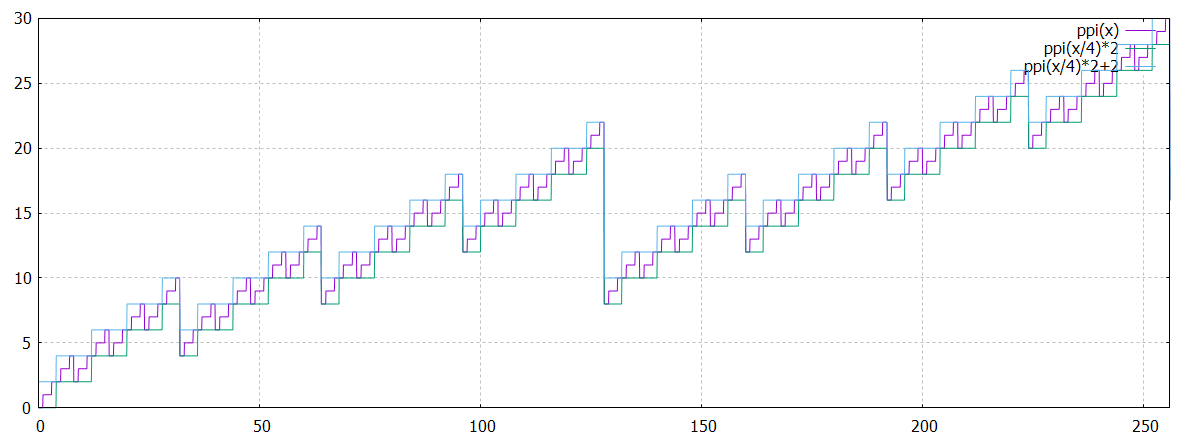
Pasted image 20240829094016.png

et
en fait pour ,
k=4; p[1:1200] ppi(x), 2**k*ppi(x/4**k), 2**k*ppi(x/4**k)+2**(k+1)-2

et aussi,

ppi(n) = ppi(n) = (n<2)?n: 2*ppi(n/4) + (n%2 + n%4)/2 La fonctionm42(x) = (n%2 + n%4)/2est périodique de période 4 et ses valeurs successives pour x%4 sont 0,1,1,2. cf https://oeis.org/A140081 Elle peut aussi s'écrirefloor(x) - floor(x/2) - 2*floor(x/4)`

Les minima locaux de (en ) valent 2**floor(log(x)/log(4.))
On pose pilog4(x) = 2**floor(log(x)/log(4.))

#TBC

bits

La fonction gnuplot suivante affiche les bits de n : Attention, ici la division des entiers est euclidienne, en javascript il faudra utiliser la fonction floor, et en gnuplot . est la concaténation de chaines, & est le AND bit par bit (bitwise AND)
bits(n) = (n==0)?"0":(n==1)?"1":bits(n/2).bits(n&1)

multiplication binaire sans retenue

Enfin a@b représente la multiplication binaire sans retenue, c'est à dire en faisant le XOR et non l'addition des résultats partiels décalés. C'est aussi la multiplication dans le corps de Galois GF[2].
@ est commutative et associative, 1 est l'élément neutre.

avec gnuplot :
mul(a,b)= (b<2)?(b&1)*a:((b&1)*a)^(mul(a,b/2)*2)
Par exemple mul(554,655) = 351878

Notons la distributivité de @ et du XOR ^ :

(a ^ b) @ c = (a@c) ^ (b@c)
(a^b)@(a^b) = a@a ^ b@b analogue à
(a^b)@(c^d) = a@c ^ a@d ^ b@c ^ b@d analogue à

On remarque aussi que 2@b = 2b et 3@b = b ^ 2b ; par exemple 3@31 = 33

R(a,b)=(a*b)-(a@b) est le vecteur des bits de la retenue dans la multiplication binaire de a et b.

Propriétés de l'insertion de bits

0\a = a@a : insertion de dans , mais aussi écriture de en base par exemple, = devient 0\1911=
a\0 = 2*(0\a) = 2a@a
2(1\x) = x\1 +3
0\x = (x\1)/2
1\x = 0\x + 2
(x\2)@(x\2) = (1\x)/4 = (x\1)/8
a\a = g(a\0) = 3(a@a) = 3(0\a) : dédoublement des bits.
Par exemple :

25    = 1 1 0 0 1, 
0\25  = 101000001  // 321 = 25 en base sqrt(2) ou 25@25
25\0  = 1010000010 // 642 = 2* 0\25
1\25  = 101000011  // 323
25\1  = 1010000011 // 643 = 25\0+1
25\25 = 1111000011 // 963, dédoublement des bits

Ces nombres n\n sont aussi ceux qui s'écrivent en base 4 avec uniquement les chiffres 0 et 3, ce qui est logique car les nombres n@n sont ceux qui s'écrivent en base 4 avec uniquement des 0 et des 1

ig(a\a) = a\0 = 2*(a@a)

Enfin

(a\b)^(b\a) = (a^b)\(a^b)
(a\b)^(b\a) = g((a^b)\0) = g(a\0)^(b\0))

Remarquons aussi que
et

Trois propriétés curieuses :

Propriétés de l'addition et de l'insertion

On a bien sûr

a\b = a\0 + 0\b
De manière surprenante,
a\b + c\d = a\d + c\b
preuve (il suffit d'écrire les bits) :

  a\b    ...a b a b
+ c\d    ...c d c d
=
  a\d    ...a d a d 
+ c\b    ...c b c b

en particulier 0\b + a\c = a\b + c@c = a\b + 0\c
et comme=a\a = 3(a@a),
a\a + 0\a = 4*a@a et donc
a\a + a\0 = 5*a@a
Enfin
(x+y)\0 = ((x+y)\(x+y))*2/3
n\0 = (n\n)*2/3 = ig(n\n)
Attention on ne peut pas en déduire ~~n*2/3 = ig(n)~~
Cette relation ne marche que pour les n qui ont tous leurs bits dédoublés.

Mais

3*(a\0) = 2*(a\a) et 3 * (0\a) = (a\a) comme nous l'avons déjà vu.

On a encore :

a\b = 2(a@a) + b@b), décomposition unique de a\b en bits pairs et impairs
0\a + 0\b = (a&b)\(a^b)
C'est-à-dire
pairs(0\x + 0\y) = x^y
impairs(0\x + 0\y) = x&y

Propriétés de la multiplication avec (*) ou sans retenue (@) et de l'insertion

J'ai trouvé les relations surprenantes suivantes :

(a\0)*(0\a) = (a\0)**2 /2 = 2*(0\a)**2 puisque a\0 = 2*(0\a) = 2a@a
(a\b)*(b\a) = 5*(0\a)*(0\b) + 2*(0\a)**2 + 2*(0\b)**2
et
(a\b)*(c\d) = (a\0)*(0\d) + (a\0)*(c\0) + (0\b)*(0\d) + (0\b)*(c\0)
=(a\0)*(0\d + c\0) + (0\b)*(0\d + c\0)
=(a\0 + 0\b) * (0\d + c\0) ce qui est évident. Bof...
mais
(a\b)*(c\d) = b@b * d@d + 2*( a@a * d@d + c@c * b@b ) + 4* a@a * c@c
=(2a@a + b@b) * (2c@c + d@d) ce qui est tout aussi trivial...

Quels sont les nombres de cette forme a@a * b@b ?

(a*b - a@b)/2 \ a@b = a@a * b@b
pairs(a@a * b@b) = a@b
impairs(a@a * b@b) = (a*b - a@b)/2 qui est la moitié de la retenue dans la multiplication de a par b, donc :
a*b = a@b + 2*impairs(a@a * b@b)
a@a * b@b = ((a*b - a@b)/2)\(a@b)

enfin

(a*b)\(c*d) = (a*b)\b + a\(c*d) - a\b intéressant
(a*b)\(c*d) = (a*b)\a + b\(c*d) - b\a par symétrie
-en fait
(a*b)\c = (a*b)\b + a\c - a\b = (a*b)\a + b\c - b\a qui est une conséquence de a\b + c\d = a\d + c\b donc a\b = a\d + c\b - c\d

remarquons aussi que si

insertion et code Gray

Si est le code Gray de x g(x)=x^(x/2), où le XOR ^ est parfois noté alors

et si est l'inverse de ,

pairs(g(a)) = g(pairs(ig(a))
impairs(g(a)) = g(impairs(ig(a))

échange des bits pairs et impairs

soit la fonction définie par swap(x)=ins(pairs(x),impairs(x))
Cette fonction échange les bits pairs et impairs.

La fonction possède les deux propriétés intéressantes suivantes :
et surtout
pour tout ,

et, pour tout
voir pir et swap

Enfin,

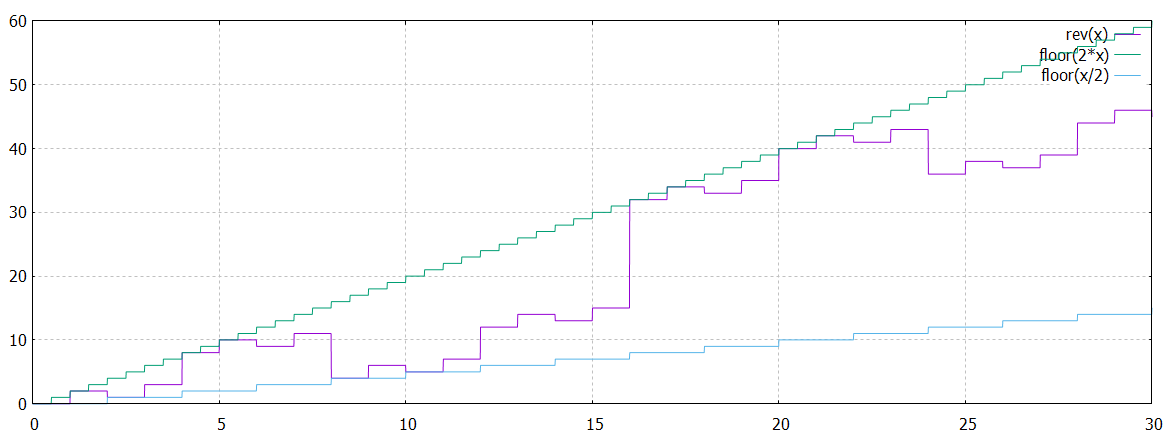
Pasted image 20240903095548.png

#A_voir : des fonctions qui ont un furieux air de famille
p [0:256]swap(x) - floor(x)/2, 2*floor(x)-swap(x), g(x), swap(g(x)) floor(x)+swap(x)

Pair, impair et passe : pir(n)

Soit la fonction

n	1	2	3	4	5	6	7	8	9	10	11
pir(n)	0	0	1	0	0	2	3	0	2	0	3

vaut 0 si et seulement si est de la forme k\0 ou 0\k c'est à dire pour n=1,2,4,5,8,10,16,17,20,21,32,34,40,42,64 = A126684
par contre uniquement pour

est un nombre premier si et seulement si n=p\1 ou n=1\p avec p premier. c'est à dire pour n=1,2,3,6,7,9,11,19,23,35,43,71,83 ... (séquence qui n'est pas dans OEIS)

Appelons l'ensemble des entiers n tels que et

théorème

Tous les nombres composés sont l'image par la fonction d'un élément de

En effet, pour un nombre composé il suffit de prendre qui est le nombre formé des bits de insérés au milieu de ceux de et on a alors

Par exemple pour ,

est donc une injection de où est l'ensemble des nombres composés

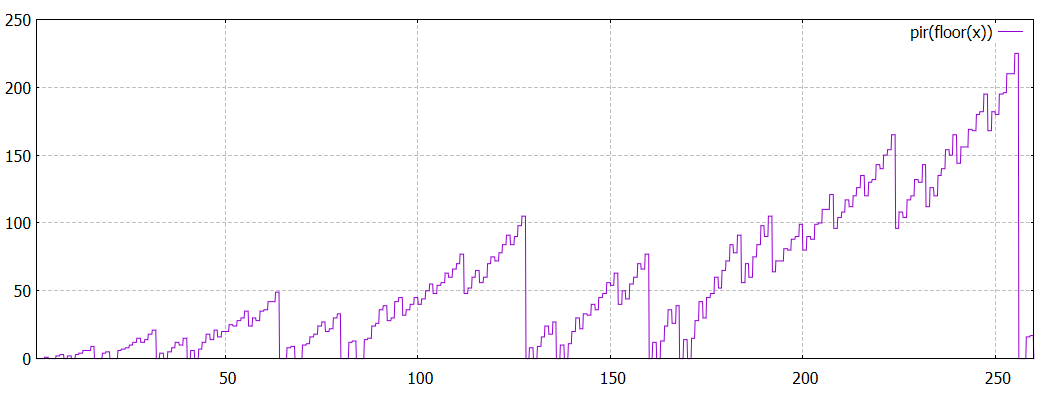
Pasted image 20240813155332.png

propriétés de

max, min

On remarque que pour tout n>8,

Les maximums sont atteints pour les et valent :
0,1,3,9,21,49,105,225,465,961 qui est la séquence https://oeis.org/A274230 : "Number of holes in a sheet of paper when you fold it n times and cut off the four corners." !

mx(n)=(n%2==0)?(2**(n/2)- 1)**2:2**n+1-3*2**((n-1)/2)

pour x=0,1,2,4,5,8,10,16,17,20,21,32,34,40, qui est https://oeis.org/A126684 et qui est l'union des valeurs de n@n et 2(n@n) ou si l'on préfère 0\n et n\0

valeurs remarquables

Si on pose R(x)=2**floor(x)-1, alors
pir(R(x)) = R(x/2)*R((x+1)/2)
et
pir(R(x)+1) = pir(2**x) = 0

pir et ins

pir(ins(x,1))= pir(ins(1,x)) = x
pir(ins(x,y)) = pir(ins(y,x)) = x*y
donc pir(ins(x,x))= x**2 donc pir(ins(g(x),g(x))) = g(x)**2
pir(g(ins(x,x))) = 0 pour tout x
pir(n**2) vaut 0 pour n = 1,2,4,8,9,16,18,32,33,36,64,66,72,128,129,132,..., soit https://oeis.org/A114400

et surtout

pir et swap

souvenons-nous que (voir échange des bits pairs et impairs)
pour tout
et pour tout ,
j'ai découvert quelque chose de curieux au sujet de la fonction :

elle est toujours positive et progresse par bonds

Pasted image 20240925182456.png

Mais surtout
k=-2;plot[0:256] 2**k*(swap(pir(x))- swap(2**k*pir(x))
est périodique de période 16 et prend pour x=0 à 15 les valeurs
0,0,0,1/2,0,0,0,3/4,0,1/4,0,3/4,0,1/4,0,1/2
pour k=-4, période 64...

pir et code gray

p[1:512]pir(g(x))/2-pir(g(x)/2)

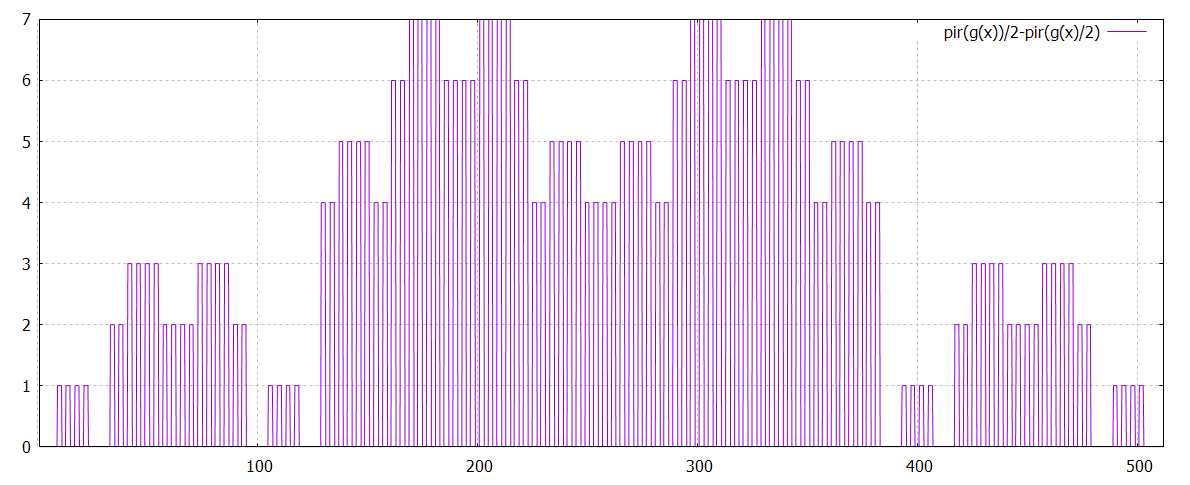
Pasted image 20240927154002.png

étrange... la fonction vaut zéro pour 4k et 4k+3. et n'oublions pas que
Ses valeurs sont très petites, et symétriques...
ça ressemble à pir(abs(impairs(x)-pairs(x)))
#TBC

equations fonctionnelles pour pir(x)

Si n est pair, est pair également. L'inverse n'est pas vrai, mais est pair et est impair.

J'ai remarqué que soit pour tout ,
Mais aussi

plot [1:200] pir(2*floor(x)+1)- (2*pir(x)+(pir(4*floor(x)+3)-pir(4*floor(x)+1)-1)/2.0)

donc

Mais surtout
donc

Enfin

Le meilleur pour la fin :

parité

vaut

0 quand x est pair, et
quand est impair

vaut :

0 quand ,
quand
quand x vaut , et
quand x vaut

Donc
et

si est pair,
- soit ,
- soit , et
- soit , et pair
si est impair, et
et en ce cas
,

On notera que
On posera cette fonction modulo 2 et 4 de . Contrairement aux autres fonctions de , celle-ci oscille toujours dans le même intervalle [0..2]

si , et
si , et
si , et
si +3, et

pir modulo 4, et autres

est périodique de période 16
idem pour et
pir(x) %4 = pir(x%16) % 4

x	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
pir(x) mod 4	0	0	0	1	0	0	2	3	0	2	0	3	0	2	2	1	0

par contre est périodique de période 8

pir(x)=4k ssi = 0,1,2,4,5,8,10,12
pir(x)=4k+1 ssi = 3,15
pir(x)=4k+2 ssi = 6,9,13,14
pir(x)=4k+3 ssi = 7,11

enfin,

est périodique de période 64
est périodique de période 9

un essai en partant de x inconnu

On prend n=291 = 3*97, donc et
donc
ou encore

On pose qui est de la forme ,
donc

mais puisque ,
donc

On pose = qui est de a forme ,
(on aurait pu remarquer que , mais bon...)

On pose qui est encore de la forme ,
on note que

On pose , qui est encore de la forme ...

On pose (de la forme 4k+1),

Or, en regardant dans la table x pour de petites valeurs de pir(x) on remarque que , et 15 est la plus petite valeur. De plus, c'est à dire qui est la profondeur de recherche.

Donc
On cherche donc le plus petit nombre tel que , et on trouve , donc

On aurait pu poser

recap

p40(x)=0
p41(x)=2*impairs(x/4)
p42(x)=2*pairs(x/4)
p43(x)=2*ppi(x/4)+1
m42(x) = (floor(x)%4 +floor(x)%2)/2
next(x)=(x%4==0)?p40(x):(x%4==1)?p41(x):(x%4==2)?p42(x):p43(x) ### pir(x) = 4*pir(x/4)+next(x)

à la fin fin de ce processus de 'descente', on a
,

(ou bien )
donc x0=4*(4*(4*4*4*5)+2)+3 = 5131 et

Donc le but du jeu consiste à calculer ces restes 1,0,0,0,2,3 "en remontant"
291 = 10203 en base 4
288 = 10200 en base 4
144 = 2100 en base 4
72 = 1020 en base 4

x0=5131 =1100023 en base 4 (nos restes)
x1=1282 = 11002 en base 4
x2= 320 = 1100 en base 4
pas concluant...

Notons que n%4 = 291%4 = 3 qui est impair,

donc il faut trouver tel que
or 145 = 4k+1
(en regardant ) on constate que
ce sera le cas si donc 1 ou 2 modulo 4
Mais il faut aussi que soit 4k+1 ??? ce qui implique
reste donc

donc soit NON (mais on ne le sait pas encore)
soit OUI (idem)
ici

donc et tous les autres termes sont pairs.
donc NON
donc
or 72=4k donc

on remonte...

On cherche tel que , le nombre à factoriser.
n est supposé être impair (291 dans notre exemple)
et même n=4k+3, donc et x0%16=7,11
donc pir(x0)-1 = 16k + 6,10 = n-1
donc (pir(x0)-1)/2 = 2*pir(x1)+ppi(x1) = 145
mais ppi(x1)=2*ppi(x2)+m42(x1) avec m42(x1) =0,1,2
donc 145= 2*pir(x1)+2*ppi(x2)+m42(x1)
m42(x1) est donc impair, donc il vaut 1 et x1%4= 1 ou 2,
donc x1=4*x2 ou x1=4*x2+2

dans le premier cas;
144= 2*pir(x1)+2*ppi(x2)
72= pir(4*x2)+ppi(x2) = 4k
et 72 = 4pir(x2)+ppi(x2) donc ppi(x2)=4k=4ppi(x3)+m42(x2)
m42(x2) est donc pair et donc il vaut 0 ou 2 et x2%4= 0 ou 3
- si x2=4k alors 72=16pir(x3)+2*ppi(x3)
  36=8pir(x3)+ppi(x3)
- à suivre...
TBC (mais ce n'est pas le cas) comment on le sait ?
- si x2=4k+3 .alors 72= 4pir(x3+2)+2*ppi(x3)+3 impossible
dans le second cas 144= 2*pir(4*x2+2)+2*pairs(x2) = 4k
72= pir(4*x2+2)+pairs(x2) = 4*pir(x3+2)+pairs(x2)
donc pairs(x2) =4k donc x2=8k+0 ou 2 (trouvé en affichant pairs(x)%4)
donc x2=4k+0 ou 1
- si x2=4k pairs(x2) = 2*pairs(x3) donc
  72 = 4*pir(x3+2)+2*pairs(x3) donc 36 = 2*pir(x3+2)+pairs(x3)
  on se retrouve devant la même alternative
  Une recherche directe des zeros de 2*pir(x3+2)+pairs(x3)=36 donne x3=80
Victoire !
#TBC ICI 01/09

ratios

j'ai étudié :

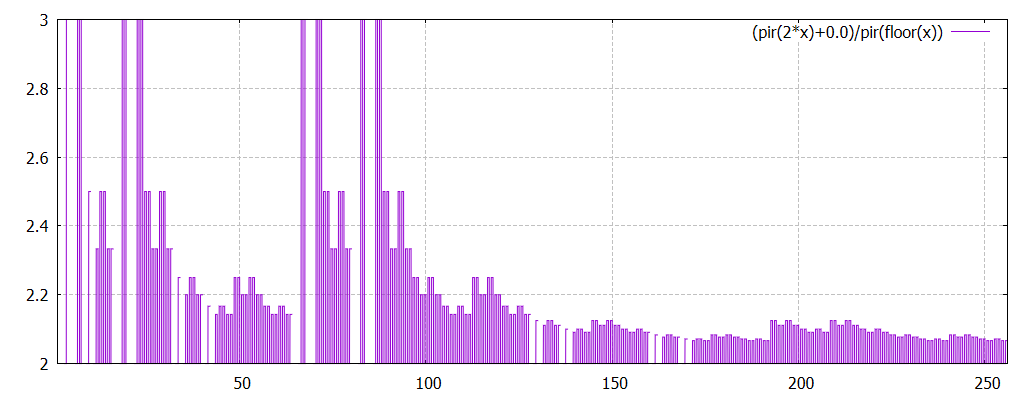
Pasted image 20240817170739.png

le ratio (quand il existe) r oscille entre 2 et 3. Il vaut exactement 2 si n est pair.
pour n impair, il semble être plus ou moins périodique lorsqu'on compare r(n) et r(4n)

Par contre r(x) = x/(pir(x)+1) est plus intéressant :

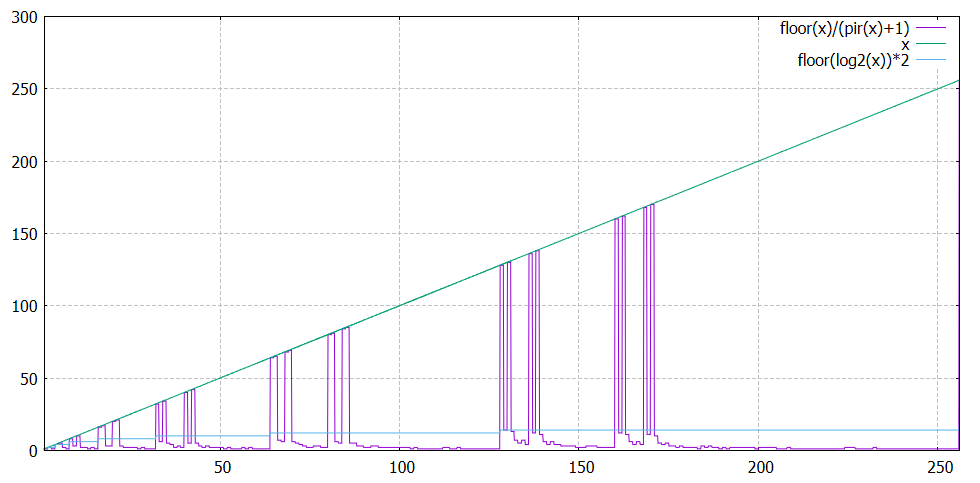
Pasted image 20240824111752.png

Le ratio ) vaut soit exactement x, soit une valeur beaucoup plus petite (mais > 0)
Il vaut pour lorsque (cf propriétés de $pir(n)$)

En cherchant tel que , on est donc sûr que l'on n'est pas dans ce cas.
Nous créons donc r2(x)=(pir(x)==0)?0:r(x)

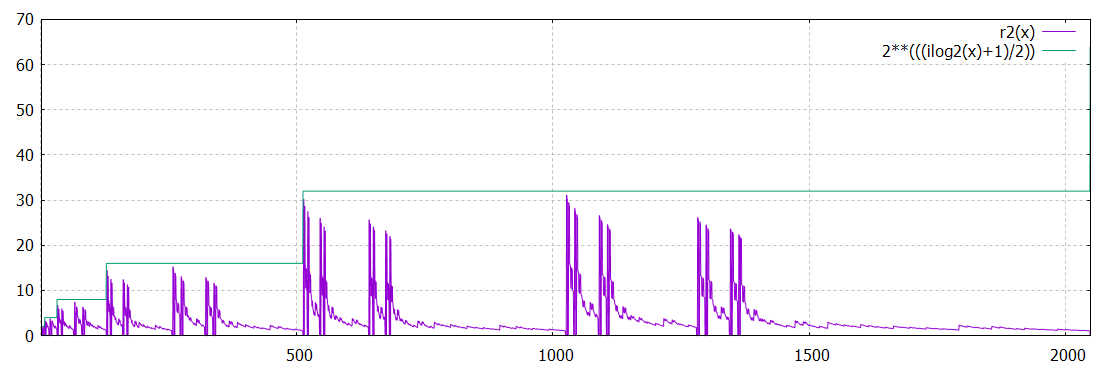
Pasted image 20240825121050.png

Les "paires de ski" qui apparaissent, c'est à dire les valeurs de r2(x) supérieures à 2**(((ilog2(x)+1)/2)-1)) pour sont, dans l'ordre, tous les x tels que pour tous les entiers entre 2 et inclus.

Pour éliminer ces "skis", nous prenons r3(x)=(pir(x)< 2**(ilog2(x)/2)+1)?0:r(x)

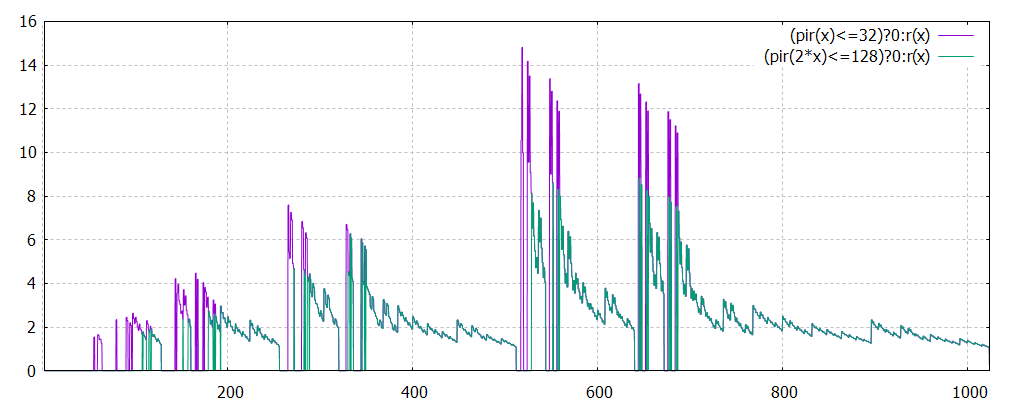
Pasted image 20240825143330.png

en fait en prenant r3(x)=(pir(x)< 2**(ilog2(x)/1.5)+1)?0:r(x) on a presque tous les ratios

petit essai

r(x) = x/(pir(x)+1) donc pir(x) = x/r(x)-1 et x=r(x)*(pir(x)+1)
Mais r(x) est quasi autosimilaire, donc
????

r3(5131)=17.5719 et r3(5131)*292=5131
mais r(5131/2.0)=17.693 ...
Partant de n=291, on a r(n)=3.38372093023256 c'est à dire
Or (cf http://sboisse.free.fr/technique/info/fractions-continues-gnuplot.php#start)

??????????
#TBC

ou alors

plot [1:2048] r2(x), 2**floor(log2(x)+floor(4*log2(log2(x)+1))-1)/floor(x)/128
plot [1:2064] log2(r2(x)+1)/ (log2(x)), log2(log2(2.0*r2(x)+1))/8
plot [3:3040] log2(r2(x)+1)/ (log2(x)), log2(2*log2(1.0*r2(x)+1))/10 + 1/log2(log2(x+1))-0.308944
notre estimation est un peu basse pour les x légèrement supérieurs aux 2**k et 2**k+2**(k-2)
ICI #TBC
rr(x)=log2(r3(x)+1)/ (log2(x))- log2(2*log2(1.5*r3(x)+1))/7+0.243838-exp(-x/500-2); plot [20:3000] rr(x)
???

pir(x)/x

est également intéressant :

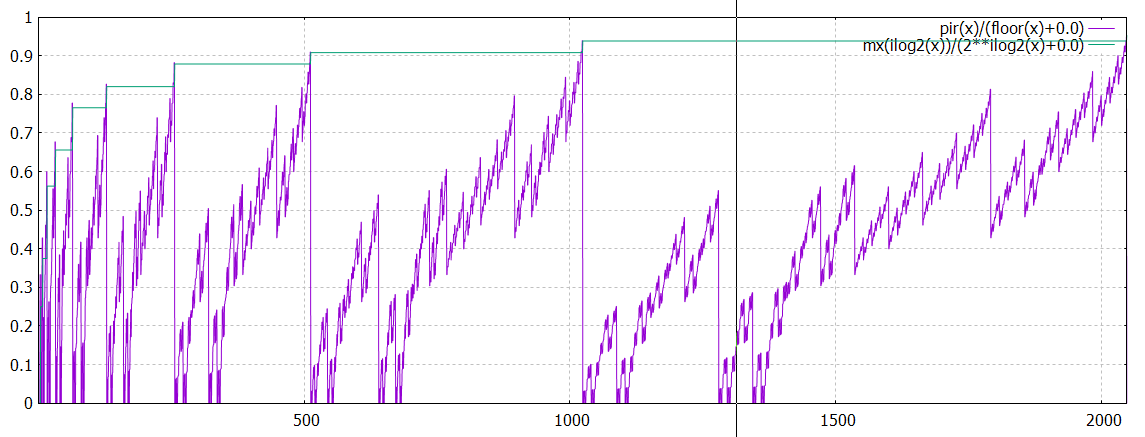
Pasted image 20240826143244.png

On peut donc "renormaliser" cette fonction pour que les maxima soit égaux à 1.
Mais attention, si donc il faut étudier
plot[16:2048] pir(x)/(floor(x+1)+0.0) / mx(ilog2(x+1)) * (2**ilog2(x+1)+0.0) (voir la définition de mx() plus haut)
Attention, pour de petits x les maxima ne sont pas exactement atteints en
en posant rr(x)= pir(x)/(floor(x+1)+0.0) / mx(ilog2(x+1)) * (2**ilog2(x+1)+0.0)
on a
rr(x)= pir(x)/(floor(x+1)+0.0) / mx(ilog2(x+1)) * (2**ilog2(x+1)+0.0)

renormalisation de pir(x) et equation fonctionnelle

Et au fait, pourquoi ne pas "renormaliser" pir(x) lui même ?
plot[20:2048] pir(x)/(mx(ilog2(x)+1)+0.0) :

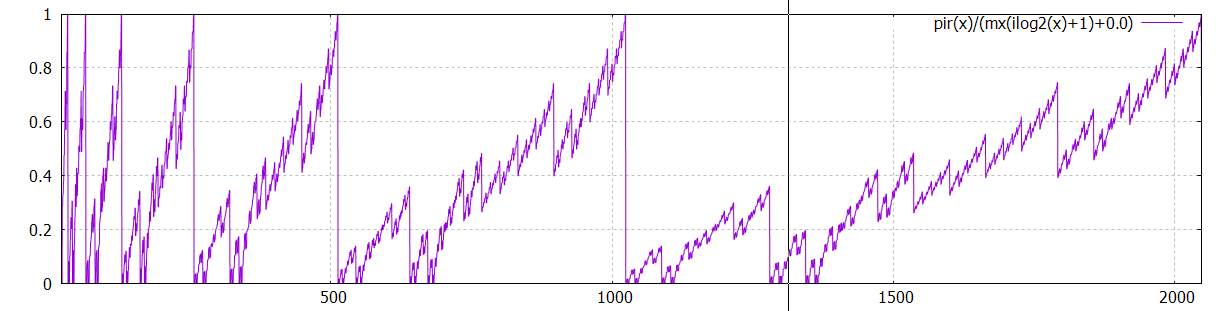
Pasted image 20240826152551.png

soit pr(x)= pir(x)/(mx(ilog2(x)+1)+0.0)
Cette fonction faut 1 pour et 0 pour
alors plot[2:2048] pr(2*floor(x))- pr(floor(x)), pr(2*floor(x)+1)- pr(floor(x)) sont très proche de zero. :

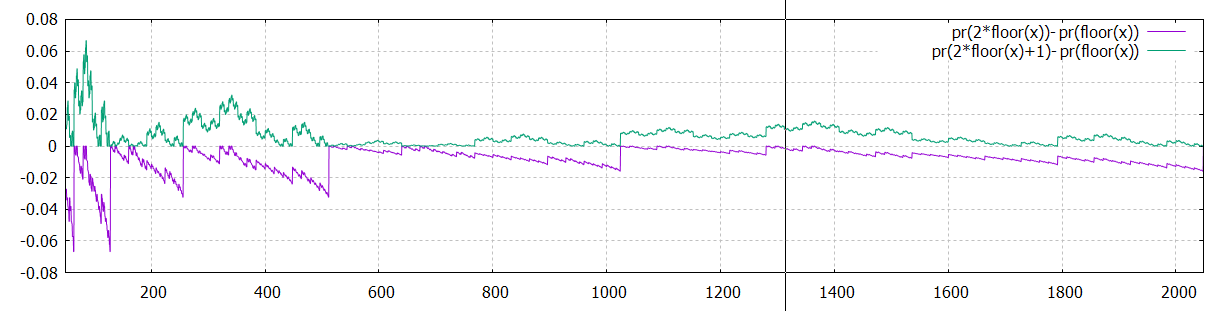
Pasted image 20240826153646.png

On pose alors xr(x)= pir(x)*(1.+pr(x))/2 "pir(x) renormalisé"
Attention, si pir(n)=0 alors xr(n) vaut 0 également.
on constate que xr(291) = 50.2688172043011
et xr(5131) = 150.79190101237 soit un ratio de 2.99971 !!

en fait 5131/2= 2565, xr(5131/2) = 149.224 ,
5131/4= 1282, xr(5131/4)*4 = 98.359, un ratio de 1,5...

Etudions directement pr(x)

pr(5131)= 0.0363704536932883 ~93/2667
pr(291) = 0.182795698924731 ~ 17/93
pr(291)/pr(5131) = 5.02593947455936 ~ 17/93 à près
or 5131=17*291+2*(93-1) ....
???
essayons avec 469=7x67 ; pr(469)=0.53333333333333 = 8/15
8x469+2x(15-1) = 3780... NOK en revanche 469x8+17x23 = 4143 et pir(4143)=469
On aussi xr(469)=190.13333 = 2852/15 ??
????

ICI 28/08 #TBC

minoration et majoration de pir(x)

Or, on peut minorer , en effet

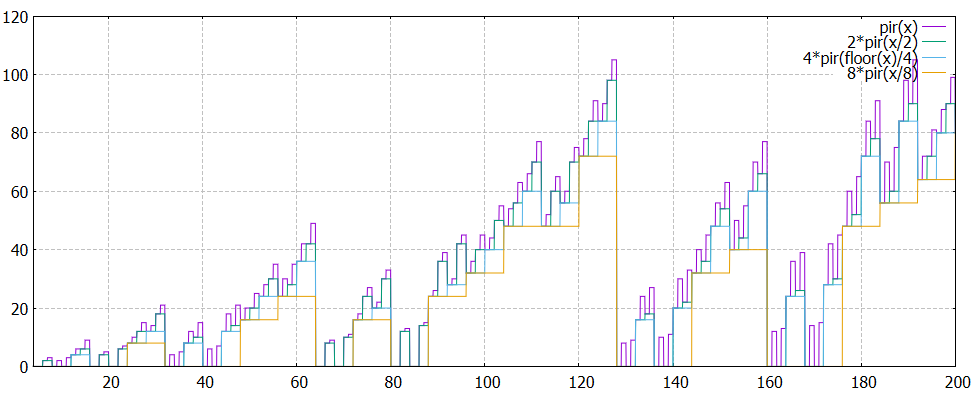
Pasted image 20240815163238.png

plot[4:200] pir(x),2*pir(x/2),4*pir(x/4), 8*pir(x/8)

Peut-on trouver des majorants ? bien sûr ! et

pour k>0 donné, on posera
down(x,k)=pir(floor(x/2**k))*2**k (minorants)
up(x,k) = pir(floor(x/2**k)*2**k+2**k-1) (majorants)
et pour tout , avec égalité si

encadrement de 2pir(x)+ppi(x)

vu que on a

En généralisant, vu que (cf ppi(x) = pairs(x)+impairs(x)), et

print [1:200] 2**(k+1)*ppi(x/4**k) , 2*ppi(x) , 2**(k+1)*ppi(x/4**k)+2**(k+2)-4

On pose ppir(x) = 2pir(x)+ppi(x)

exemple

cherchons à factoriser :
on cherche tel que on sait que
on suppose que x < 2n.

...
On trouve
et Victoire !

Bon en fait c'est pas si simple, il n'est pas vrai que le cherché soit toujours plus petit que 2n. (il est plus petit que )

Supposons qu'on l'ait trouvé, donc . Comme est impair, , donc
et donc avec l'inconnue à trouver.
Il est remarquable que si on pose alors est très petit...

Pasted image 20240817210350.png

ça fait penser ) un battement de signaux sinusoïdaux... ou à Mandelbrot...
en fait pour tout entier,

plot [0:255] f(x/2)*2-f(x),(pairs((x/2))+floor(x)%2)*(-1)**floor(x)
plot [0:255] (f(x)-f(x/2)*2)*((floor(x)%2==0)?-1:1), pairs((x/2))+(floor(x)%2)
et même, pour tout k positif,

Donc
#TBC

formules pour pir(x)

16:
plot [0:256] pir(floor(x)*16+0)-pir(floor(x)*16), 0
plot [0:256] pir(floor(x)*16+1)-pir(floor(x)*16), impairs(x)*4
plot [0:256] pir(floor(x)*16+2)-pir(floor(x)*16), pairs(x)*4
plot [0:256] pir(floor(x)*16+3)-pir(floor(x)*16), pairs(x)*4 + impairs(x)*4+1
plot [0:256] pir(floor(x)*16+4)-pir(floor(x)*16), impairs(x)*8
plot [0:256] pir(floor(x)*16+5)-pir(floor(x)*16), impairs(x)*12
plot [0:256] pir(floor(x)*16+6)-pir(floor(x)*16), pairs(x)*4+ impairs(x)*8+2
plot [0:256] pir(floor(x)*16+7)-pir(floor(x)*16), pairs(x)*4+impairs(x)*12+3
plot [0:256] pir(floor(x)*16+8)-pir(floor(x)*16), pairs(x)*8

plot [0:256] pir(floor(x)*16+11)-pir(floor(x)*16), pairs(x)*12 + impairs(x)*4+3

plot [0:128] pir(floor(x)*16+15)-pir(floor(x)*16), pairs(x)*12 + impairs(x)*12+8

k=3;r=1;plot [1:256] pir(2**k*floor(x)+r)-2**k*pir(x) - (2**(k/2+1)*impairs(x)*impairs(r)+2**(k/2)*pairs(x)*pairs(r)+pairs(r)*impairs(r))

en fait la formule générale est, pour et Attention, signifie en fait :

si est pair :

si k est impair :

et pour k=1, (donc r=0 ou r=1) :
comme nous l'avions vu plus haut

Enfin, si c'est à dire impair, alors

un petit calcul...

prenons
(n-1)/2=145 est impair;
en fait n=2x145+1=71x4+3= 368+3 = 1816+3 = 9x32+3 (k=5)
choisissons k=5 et essayons tous les x entre 1 et 18

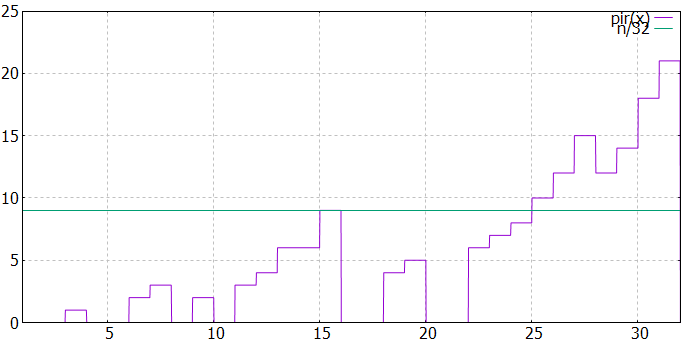
Pasted image 20240819171138.png

Nous constatons que pir(15)=n/32. =9
Nous ignorons encore r, mais puisque k est impair,
avec
On pose
d1(x,k,r)=2**(k/2+1)*impairs(x)*impairs(r) + 2**(k/2)*pairs(x)*pairs(r) + pairs(r)*impairs(r)
d2(x,k,r)=2**(k/2)*pairs(x)*impairs(r) + 2**(k/2)*impairs(x)*pairs(r) + pairs(r)*impairs(r)
d(x,k,r)=(k%2==0)?d2(x,k,r):d1(x,k,r)
on essaye tous les r entre 1 et 32... finalement
pour k=5, r=11, y=160, 2**k*pir(y)+d(y,k,r) =n
idem pour k=7, r= 11, y=40 et
k=9, r=11, y=10 et
k=10, r=11,y =5
k=10;r=x%(2**k); y=x/2**k; pr k,r,y, 2**k*pir(y)+d(y,k,r), 2**k*y+r qui donne 10 11 5 291 5131
k=11, r=1035, y=2 !
Et bien sûr, pour toutes ces valeurs, et soit les diviseurs de .

Le problème est donc de trouver les bons k,r et y...

Or nous avions trouvé avec une division entière mais comme n%32=3, on a 32pir(15)=n-3
donc le x cherché est vaut avec tel que

Donc

donc doit être divisible par 32
Or, si on se souvient que ce nombre est de la forme , il faut
De plus,

Pas simple... Peut être en le faisant à l'envers ?

en partant de xx=5131, n=291

Nous savons que pir(15)=n/32=9 et pir(5131)=n=291
5131=2*2565+1
donc 2*pir(2565)+pairs(2565)=n et pairs(2565)=3
2565=2*1282+1
donc 2*pir(1282)+pairs(1282)=pir(2565)=144 et pairs(1282)=48
pir(1282) = 2*pir(641)
641=320*2+1
2*pir(320)+pairs(320)=pir(641)=24 et pairs(320)=24
pir(320)=0 = floor(n/2**9 (et 9 est le plus petit nombre)

En remontant...
il faut essayer tous les k entre 1 et 2**9 (en fait uniquement ceux qui ont des pairs(k) différents donc 31 possibilités) et les prendre comme "racine". je ne teste l'idée que pour k1=320, et donc pairs(k1)=24
Donc l'essai suivant (N°1) sera 2k1+1=320*2+1=641 et
pour l'essai 2 nous prenons soit k2=1282, soit 1283
pir(1282)=48 et pir(1283)=49 Aucun des deux n'est proche d'un n/2**r donc on continue

si k2=1282, k3=2*1282+1=2565 et

#TBC

programme

version 1 :
cf factopir.js (Fichier sur D)(lien privé)dans mon ordi... (version 1, qui utilise les majorations et minorations de pir(x))

si n=4k+1 ou 4k+3, donc n est impair, donc x=4k+3 et
n= pir(x)=4*pir(x/4)+2*ppi(x/4)+1
donc ppi(x/4) %4 = 0 donc x/4 = 16k+0,1,7,11,12 ??

si n=4k+2....

#TBC

inversion directe de pir

Vu que , je croyais mais non, en revanche
= 3,6,12,24,72,264,1032,4104,16392,65544,262152
; et pour ,

Cette suite 8,9,12,13,24,25,28,29 est A131864 "la suite telle des nombres n tels qu'une certaine fonction z(n) a une partie imaginaire <0".... oops...
et aussi
en fait,

Théorème

pour entier > 2,

pour les n impairs, inv(n) est plus compliquée...
mais of course.
plot [2:200] inv(2*floor(x)+1), ins(x,1)*2

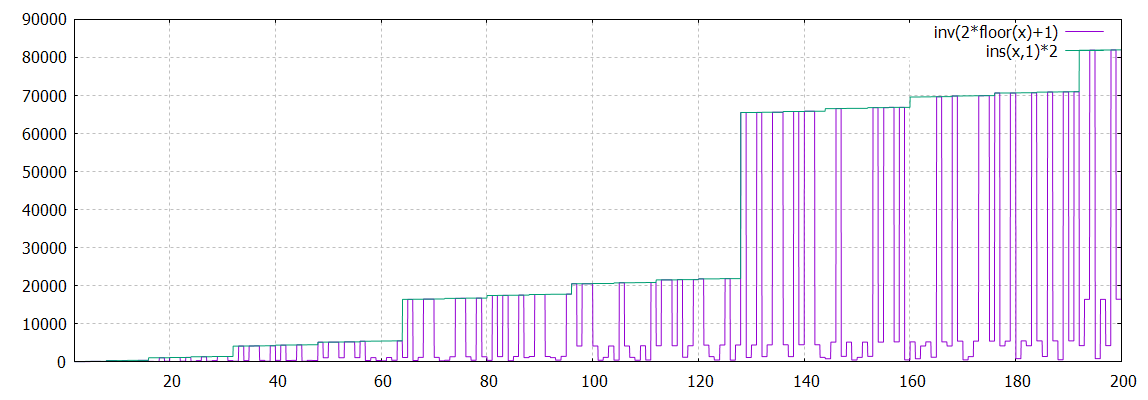
Pasted image 20240906132810.png

inv(2*floor(x)+1) = ins(x,1)*2+1 pour beaucoup de valeurs 1,2,3,5,6,8,9,11,14,15,18,20,21,23...
et ins(x/3,0)*2 pour beaucoup d'autres

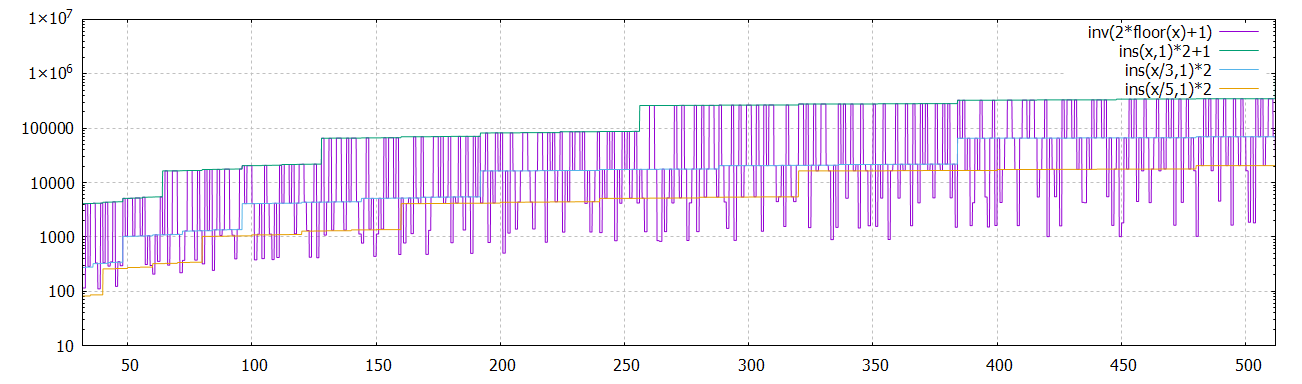
Pasted image 20240906231423.png

#TBC 23/08

Si est impair, et si donc , alors = 4k+3 et , c'est à dire

donc et on cherche tel que
c'est à dire
ou encore
donc
voir encadrement de 2pir(x)+ppi(x)
or

#TBC ICI 06/09/224

que vaut inv(2**k+x) ? et pir(3*2*k+n) ?
si n < 2**k
pairs(3*2**k+n) = 2**ceil(k/2.)+pairs(n)
impairs(3*2**k+n) = 2**floor(k/2.)+pairs(n)
donc pir(3*2**k+n) = 2**k + pairs(n)*2**floor(k/2.) + impairs(n)*2**ceil(k/2.) + pir(n)
si n=1, pir(3*2**k+1) = 2**k + 2*floor(k/2.) ???

Mais si
alors pairs(3*(2**a+2**b)) = 2**((a+1)/2)+2**((b+1)/2) sauf si a=2k, b=2k+1 ou a=2k+1, b=2k (donc OK si a=2k+1,b=2k+2
et impairs(3*(2**a+2**b)) = 2**(a/2)+2**(b/2) sauf si a=b ou a=2k, b=2k-1 ou a=2k-1, b=2k

Donc pir(3*(2**a+2**b) = ????
ICI 02/09/2024 #TBC

etude directe de inv(n)

En fait on peut définir si on connait déjà la factorisation de par :
insf(n,p)=ins(p,n/p)
inv(x)=insf(floor(x),facto(x))
ou encore inv(x)=ins(facto(x),x/facto(x)

Pasted image 20240903112329.png

Où facto(x) renvoie le plus petit facteur premier de x, et 1 pour les nombres premiers.

inv(0)=1, inv(1)=3, inv(2)=6, inv(3)=7, inv(4)=12, inv(5)=19
et on a

Si est premier,
Si , alors

Si :

est pair ssi x=4k
ssi x=4k+2, ssi x=est impair
ne vaut jamais 2.

SI on se souvient que , on a
j'ai découvert et

Et aussi

Réciproque de : inv(n)

Soit l'ensemble des entiers positifs tels que Cet ensemble n'est pas vide puisqu'il contient au moins n\1 et 1\n

L'espoir est que, si on peut trouver un tel , alors si pair(x) et impair(x) >= 2, on aura factorisé .

Rappelons-nous que si l'on sait factoriser , alors

insf(n,p)=ins(p,n/p)
inv2(x)=insf(floor(x),facto(x))
pr inv2(291) # 5131

soit inv(n) la fonction qui retourne le plus petit (ou presque..) tel que

inv(0) = 0
inv(1) = 3
inv(2) = 6
inv(3) = 7
inv(4) = 12
inv(5) = 19
inv(6) = 13
inv(7) = 23
inv(8) = 24
inv(9) = 15

et la suite 0,3,6,7,12,19,13,23,24,15 n'est bien sûr (?) pas dans OEIS...

x pour de petites valeurs de pir(x)

Dans la liste ci-dessous les nombres entre sont ceux pour lesquels ni ni ne valent ni 1 ou :
pour l'union des valeurs de n@n et 2(n@n) ou si l'on préfère 0\n et n\0 (cf propriétés de $pir(n)$)
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour et c'est tout
pour
pour et c'est tout
pour
pour
... les 2 derniers nombres de chaque liste donnent 1xn
les premiers termes donnent la suite
pour n pair, la sous-suite semble être celle des nombres dont l'expansion binaire commence par 11 ?
pour n impair (le cas intéressant), on a la sous-suite qui n'est pas dans OEIS

Si est pair, donc doit aussi être pair. (cf parité)

Mais si est impair, et si avec donc x forcément impair, alors doit être de la forme

modulo

pour x =0 et c'est tout
avec pour x = 0,1,3,6,14,25,91,99,104,225,232,315,377
avec pour x = 0,1,2,3,4,7,8,12,16,24,32,64,124,128,248,256
avec pour x =
0,2,4,18,36,144,288,572,578,1144,1156,1168
avec pour x = 0,27,54,108,216,432,558,864,1728
avec pour x = 0,4,5,9,10,20,38,40,76,80,160,320,637,640,1260
avec pour x = 0,15,31,62,124,1507,3944,
avec pour x = 0,15,31,62,124,1507,3944,
avec pour x = 0,2453,15775,31550,...

Avec gnuplot :

ok(x,k,r)=(r<0)?-1:(pir(k*x+r)==x)?0:ok(x,k,r-1)
f(x)=ok(x,k,k-1)
zeros(a,b)=(a>b)?"":(f(a)==0)?"".a.",".zeros(a+1,(a+b)/2).zeros((a+b)/2+1,b):zeros(a+1,(a+b)/2).zeros((a+b)/2+1,b)
k=11 #par exemple
print zeros(0,10000)

pour x=4k et pour 2, =1 pour les autres
pour x=4k
pour x=4k+2
pour x=0,2 et c'est tout
pour x impair
Les autres modulo ne sont pas périodiques bien qu'il y ait des sections identiques dans le graphe...

composition

Soit une fonction telle que

donc
ou si l'on préfère
Attention ce n'est pas le cas de , en effet
Il existe plusieurs de ces fonctions, on prendra la plus petite valeur de telle que

pour : 1,3,6,7,12,19,13,23,24,15,25,71,28

or pour x=3,6,12,24,48,96... ce qui se comprend car en binaire ces sont de la forme 110..0 et via la fonction , un des deux 1 tombe dans l'escarcelle de au rang ceil(k/2.), l'autre dans la besace de au rang floor(k/2.).
donc

inv et swap

j'ai découvert que inv(x) et swap(inv(x)/2) sont très proches pour des nombres qui ont de petits diviseurs : (image en échelle logarithmique)

Pasted image 20240925203847.png

Les valeurs successives (pour ) sont 2,2,2,2,6,2,6,2,6,8,6,2,6,2,6,8,6,2,6,2,6,8,6,2,6,26...

#TBC

inv(pir(x))

pour x=0,1,2,4,5,8,10,16,17,20,21,32,34,40,42 (cf max, min)
est pair pour x=6,9,12,18,24,26,28,33,36,37,44,48,49 (pas dans OEIS)
pour x=1,3,6,7,12,13,15,19,23,24,25,27,28,29,31 (pas dans OEIS)
pour x=2,3,9,11,12,14,15,35,36,38,39,43,44,46 (pas dans OEIS)
ou pour presque tous les sauf 3,12,15,51,63,207,243,771,783,831,1011,1023,3123 cf https://oeis.org/search?q=12%2C15%2C51%2C63%2C207%2C243%2C771%2C783%2C831&go=Search

pour x=1,2,4,5,8,10,16,17,20,21,32,34,40,42... qui est https://oeis.org/A126684, soit si est de la forme k\0 ou 0\k ce qui implique pir(x)=0

il y a quelque chose de bizarre dans
plot [0:1024][1:1024] inv(pir(x)), min(x,swap(x))
en effet ces valeurs sont égales pour beaucoup de x :

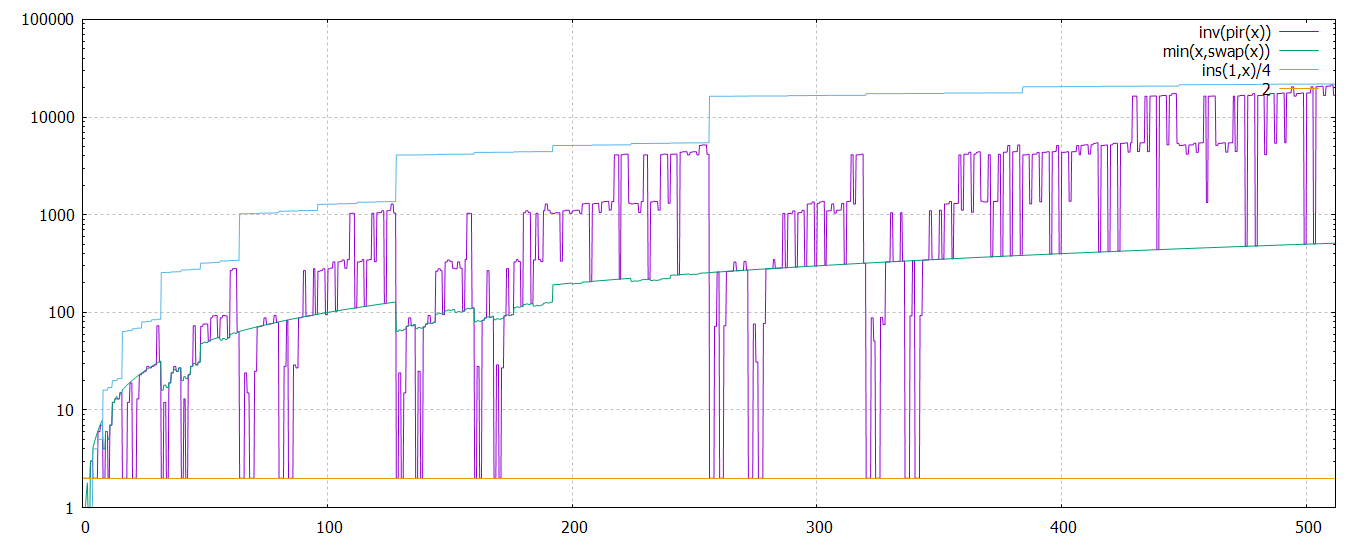
Pasted image 20240925211907.png

#TBC

minoration et majoration de inv(x)

majoration :
= 2,3,6,7,18,19,22,23,66,67,70,71,82,83,86,87,258

minoration :
il semble que inv(x) > 1.6*2**(ilog2(x)) ?????
ou bien inv(x) > x ?

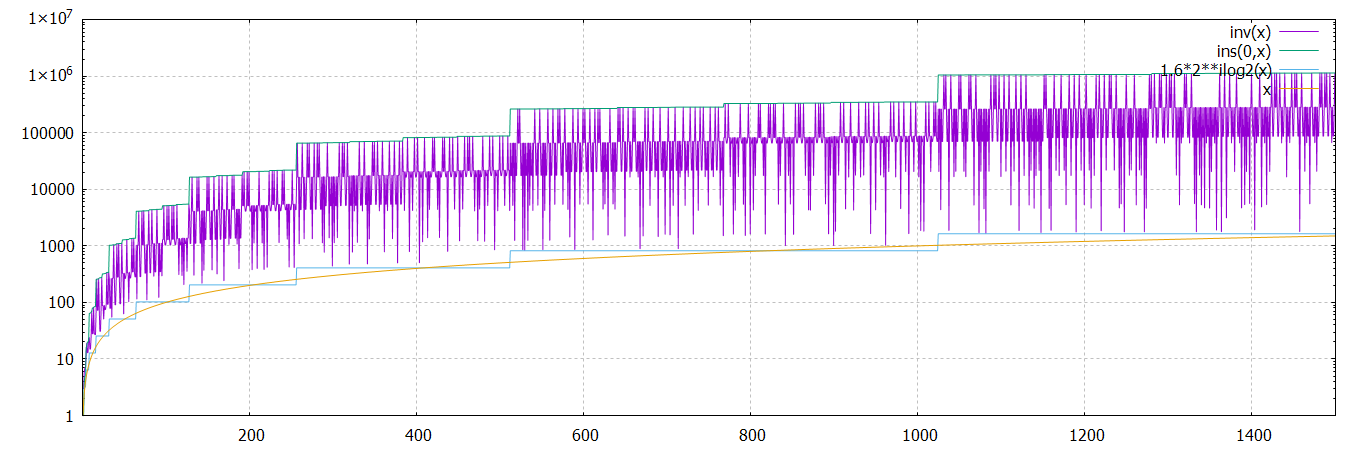
Pasted image 20240925210930.png

#TBC

les étages

les maxima locaux de sont les
"l'étage 2 juste en dessous" est pour x>31
en fait inv(x) n'est jamais proche de ins(1,x)/3
"l'étage 3 juste en dessous" est pour x>63
et ins(1,291/3)+8 = inv(291) = 5131

WOW ! quoique...

en fait on utilisé les fonctions
h1(x)=(abs(inv(x)-ins(1,x))<100)?inv(x)-ins(1,x):-1
apériodique, rend les valeurs 0 et -1

h2(x)=(abs(inv(x)-ins(1,x/2))<100)?inv(x)-ins(1,x/2):-1
périodique (période 2) rend les valeurs 6 et -1 sauf pour 11,13,21,25,27,51,57,63

h3(x)=(abs(inv(x)-ins(1,x/3))<100)?inv(x)-ins(1,x/3):-1
périodique, prend les valeurs 8 et -1 sauf pour un certain nombre de petites valeurs (<63)

h4(x)=(abs(inv(x)-ins(1,x/4))<100)?inv(x)-ins(1,x/4):-1
apériodique, rend la valeur -1 pour tous les x >186, sauf pour 245 ?

h5(x)=(abs(inv(x)-ins(1,x/5))<100)?inv(x)-ins(1,x/5):-1
périodique, rend les valeurs -1 et 32 pour x>94 sauf 119 et 133

h6(x)=(abs(inv(x)-ins(1,x/6))<50)?inv(x)-ins(1,x/6):-1
apériodique

h7(x)=(abs(inv(x)-ins(1,x/7))<50)?inv(x)-ins(1,x/7):-1
périodique, rend les valeurs -1 et 40

res(k)=(k<=1)?0:(k==2)?6:(k==3)?8:(k==4)?0:(k==5)?32:(k==6)?0:40
inv2(x,k)=ins(1,x/k)+res(k)
divise(x,d)=(d!=x && d != 1 && x%d==0)
ok(x,k)=divise(x,pairs(inv2(x,k)))?pairs(inv2(x,k)):-1
test(x,k)=(k>7)?"echec":ok(x,k)>0?ok(x,k):test(x,k+1)
fact(x)=test(x,1)
fact(291) # 97
fact(13) # echec

On n'a pas fait mieux que le crible d'Erathotène ?? sauf que les étapes suivant 7 ne rendent que -1...

a priori rend les valeurs #TBC

ppi(inv(x))

intéressant :

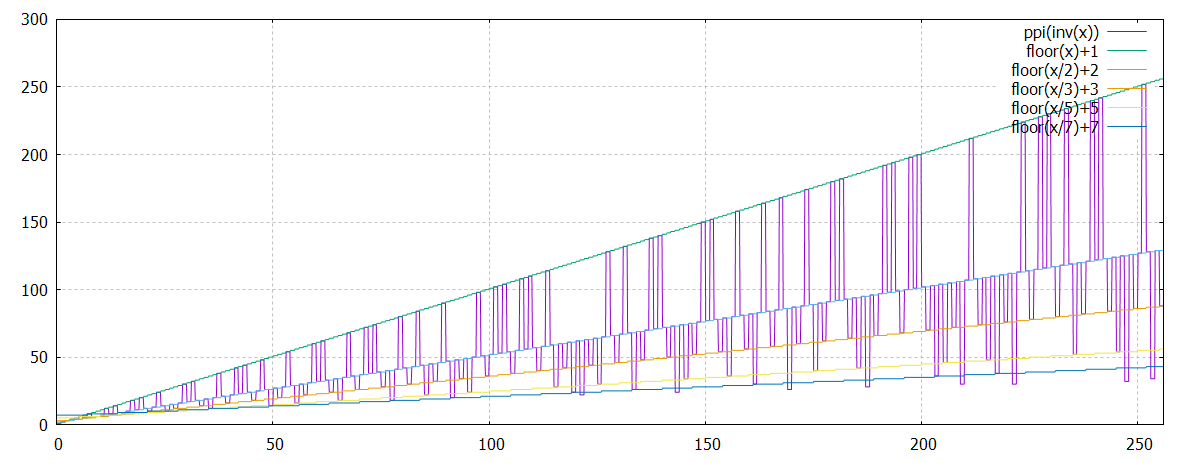
Pasted image 20240928162624.png

Cette fonction est quasiment !
en fait,

C'est à dire la somme des deux diviseurs de
En effet, si , ou encore
donc of course.

equations fonctionnelles pour inv(x)

oscille autour de 0 :
plot [1:255] (inv(4*floor(x)+3)-(inv(4*floor(x)+1))-1)

fonction c(x)

soit la fonction
qui ne produit que des nombres composés, et les produit tous.
Si , avec , alors et
Si on veut factoriser , il faut trouver tel que et on alors et

n	0	1	2	3	4	5	6	7	8	9	10	11
c(n)	4	6	6	9	8	10	12	15	8	12	10	15

...of course (?) pas dans OEIS.

Comme pour , si est pair, est pair et est pair et est impair. Donc si est impair, alors

Les 20 premières valeurs de c(x) sont
4,6,6,9,8,10,12,15,8,12,10,15,16,20,20,25,12,14,18,21,16

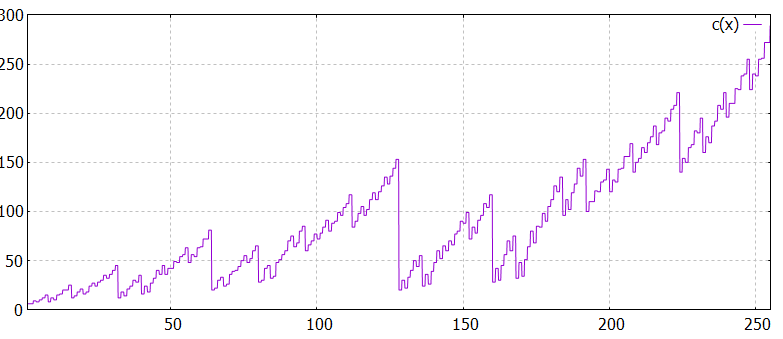
Pasted image 20240818210553.png

relation avec pir(x)

propriétés de c(cx)

Contrairement à , les minima (en ) ne valent pas 0 mais
6,8,8,12,12,20,20,36,36,68,68,132,132,260,260 (pas dans OEIS),
cependant

et les maxima (en ) sont :
6,9,15,25,45,81,153,289,561,1089,2145,4225,8385,16641,3315
pas dans OEIS non plus, mais pour les indices pairs on a , et pour les indices impairs (les nombres triangulaires d'indice ) ??

En fait pairs(2**k-1) = 2**((k+1)/2)-1 et
impairs(2**k-1)=2**(k/2)-1
Donc nos maximas sont les 2**((k+3)/2) + 2**((k/2+1))+mx(k)
borne sup :
p[0:1024] c(x), 2**((ilog2(x)+3)/2) + 2**((ilog2(x)/2+2))+mx(ilog2(x)+1)

parité de c'x)

c(x) est pair pour x=4k+0,1,2
c(x) est impair pour x =4k+3
c(2n) est toujours pair
c(2n+1) est pair ssi n est pair

equations fonctionnelles pour c(n)

j'ai trouvé les relations suivantes :

js

function pairs(n) {
// pairs(b)= (b<=0)?0:(b%2)+pairs(b/4)*2
	if (n==0) return 0;
	if (n==1) return 1;
	return n%2+pairs(Math.floor(n/4))*2;
}
function c(n) {
	if (n==0) return 4;
	if (n==1) return 6;
	if (n%2 ==1) {
		let m = (n-1)/2;
		return c(m)+c(n-1)/2;
	}
	// n pair
	return 2*c(n/2)-2*pairs(n/2)-4;
}
console.log(c(2),c(3),c(4),c(5),c(6),c(7),c(8));

inversion directe de c(x) : invc(x)

on pose invc(x)=ins(facto(x)-2, x/facto(x)-2)

Pasted image 20240928173107.png

ça ressemble beaucoup à inv(x) mais c'est différent

propriétés de invc(x)

cette différence vaut 0 pour tous les nombres pairs, et 3 pour presque tous les impairs, mais parfois 15,51,195, 207,255...

c(invc(x))

Pasted image 20240928173643.png

vaut si est premier, et sinon

invc(c(x))

C'est plus compliqué...

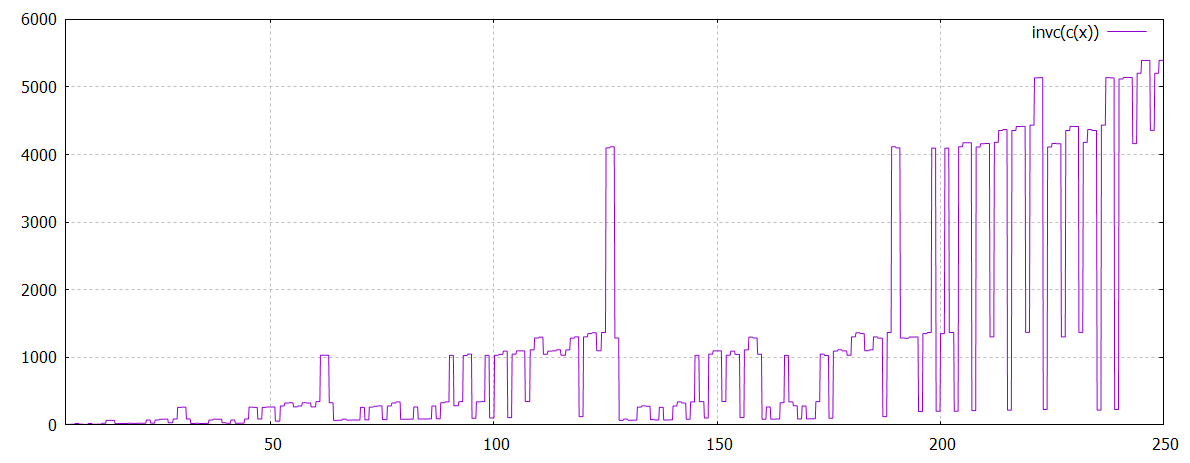
Pasted image 20240928173923.png

exemple

n=291=3*97, p=3, q=97, x=ins(p-2, q-2)=4439, c(x)=n
n/2=2219, c(2219)*2=294
n/4=72, c(72)*4 = 160 donc pas génial
mais n=2*145+1 donc

ICI 27/08
p[200:5160] c(x)- c(2*floor(x)+0)/2, c(x)- c(2*floor(x)+1)/2
c20(x)=c(x)- c(2*floor(x)+0)/2
p[200:5160] c20(x), c20(x/4)*2 -> oscille entre -1 et -2
c21(x)=c(x)- c(2*floor(x)+1)/2
p[200:5160] c21(x), c2(x/4)*2 -> oscille entre 0, -1 et -2

autre idée

en fait au lieu d'utiliser les fonctions pairs et impairs on pourrait multiplier des groupes de 2,4, 8 bits etc.

ABCDEFGHILKLMNOP -> pir  -> ACEGIKMO * BDFHJLNP
                 -> pir2 -> ABEFIJMN * CDGHKLOP  
				 -> pir4 -> ABCDIJKL * EFGHMNOP
				 -> pir8 -> ABCDEFGH * IJKLMNOP

#TBC

questions

Riemann

Comme c(x) produit tous les nombres composés, et uniquement eux (mais avec des doublons) peut-on compter les doublons de c(x) de manière à déterminer le nombre de nombres premiers inférieurs à x et prouver la conjecture de Riemann ?
pour , les valeurs de telles que sont : (pour les autres valeurs, pas de doublons)

x	8	9	10	11	14	16	20	21	24	32	33
y	4	6	5	7	13	6,9	12	18	22	6,9,16	18,21

Pas très clair...
Une fonction qui compte les doublons :
dd(x,y)=(y<=1)?0:(c(floor(x))==c(floor(y)))?1+dd(x,y-1):dd(x,y-1)
doublons(x)=dd(floor(x),floor(x)-1)

Premiers jumeaux (twin primes)

si n est premier, les valeurs telles que sont telles que soit , soit Peut-on utiliser ce résultat et , et aussi le fait que le nombre situé entre deux premiers jumeaux est nécessairement un multiple de 3, (donc que deux premiers jumeaux sont tels que pour prouver la conjecture des nombres premiers jumeaux ?

Goldbach

A tous les nombres pairs on peut associer un ensemble de nombres {x} tels que donc ou est pair. peut on utiliser ce fait pour prouver la conjecture de Goldbach ?

Dubner

La conjecture de Dubner suppose que tous les nombres pairs supérieurs à 4210 sont somme de deux nombres premiers ayant un jumeau. Elle implique donc twin primes et Goldbach.

Comme et que ssi ou ,
p est premier ssi
or si p est impair, inv(p)%4=3
en fait, x est premier ssi inv(x)/(ins(0,x)+0.0) > 1 et même > 0.25 !!!!

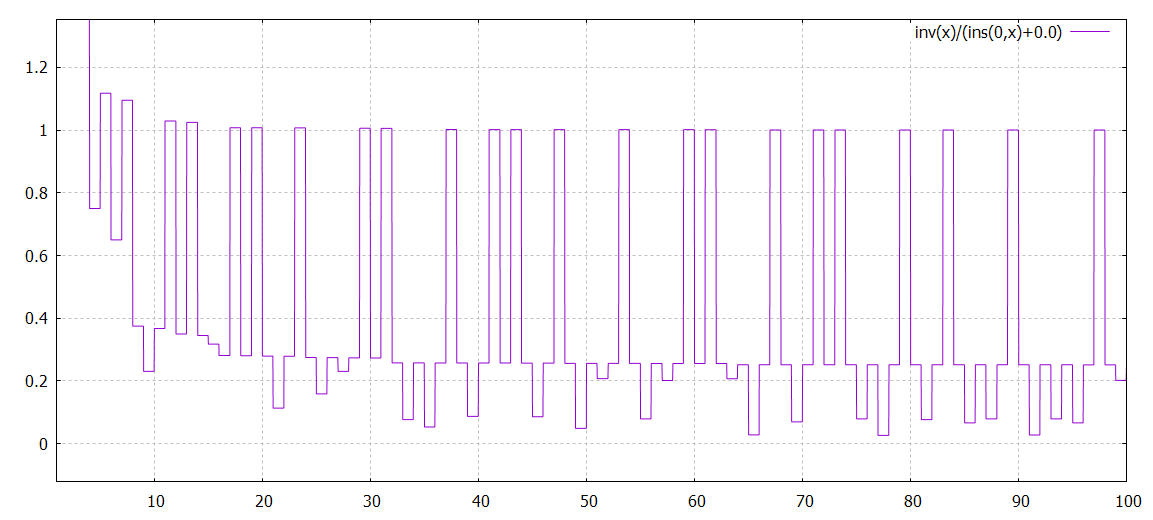
Pasted image 20240907163943.png

#TBC ICI 07/09

gnuplot

Liste des fonctions utilisées dans ce document :

bits(n)=bits1(floor(n))." "
bits1(n) = (n==0)?"0":(n==1)?"1":bits1(n/2).bits1(n&1)
ins(a,b) = (a==0&&b==0)?0:(b&1)+2*(a&1)+4*ins(a/2,b/2)
pairs(b)= (b<=0)?0:(b%2)+pairs(b/4)*2
impairs(a)= (a<=1)?0:((a/2)%2)+impairs(a/4)*2
ppi(x)=pairs(x)+impairs(x)
mul(a,b)= (b<2)?(b&1)*a:((b&1)*a)^(mul(a,b/2)*2)
ilog2(x)=floor(log(x)/log(2.))
pilog2(x) = 2**floor(log(x)/log(2.))
pilog4(x) = 2**floor(log(x)/log(4.))
pir(n)=pairs(n)*impairs(n)
mx(n)=(n%2==0)?(2**(n/2)- 1)**2:2**n+1-3*2**((n-1)/2)
facto1(d,n)=(n%d==0)?d:(d*d>n)?1:facto1(nextprime1(d),n)
facto2(n) =(n<=1)?1:(n%2==0&&n!=2)?2:(n%3==0&&n!=3)?3:(n%5==0&&n!=5)?5:(n<49)?1:facto1(7,n)
facto(n) =facto2(floor(n))
nextprime1(n)=(facto2(n+2)==1)?n+2:nextprime1(n+2)
nextprime2(n)=(n<2)?2:(n%2==0)?nextprime1(n-1):nextprime1(n)
nextprime(n) =nextprime2(floor(n))
insf(n,p)=ins(p,n/p)
inv(x)=insf(floor(x),facto(x))
R(x)=2**floor(x)-1
swap(x)=ins(pairs(x),impairs(x))
c(x)=(pairs(x)+2)*(impairs(x)+2)
invc(x)=ins(facto(x)-2, x/facto(x)-2)

Voir aussi:

Mes recherches sur la factorisation
Mes recherches mathématiques

page créée le 18/03/2025 à 15:09

modifiée le 25/05/2025 à 12:05

Commentaires

Commentaires (0) :

Page :

Ajouter un commentaire (pas besoin de s'enregistrer)

En cliquant sur le bouton "Envoyer" vous acceptez les conditions suivantes : Ne pas poster de message injurieux, obscène ou contraire à la loi, ni de liens vers de tels sites. Respecter la "netiquette", ne pas usurper le pseudo d'une autre personne, respecter les posts faits par les autres. L'auteur du site se réserve le droit de supprimer un ou plusieurs posts à tout moment. Merci !
Ah oui : le bbcode et le html genre <br>, <a href=...>, <b>b etc. ne fonctionnent pas dans les commentaires. C'est voulu.

< Retour en haut de la page

Journal d'un Terrien