Journal d'un Terrien
Web log de Serge Boisse
On line depuis 1992 !
Liste des tags :
__________________
http://sboisse.free.fr/science/maths/Mes Recherches mathematiques/iteration/Tent map.php
Tent map
Voir aussi: MathJax
tent map.txt (Fichier texte sur NAS)(lien privé) ou en local : tent map.txt(lien privé)
l'application logistique
J'ai découvert une étrange corrélation entre la Tent Map et le code de Gray :
La Tent map, c'est l'application
Dans ce qui suit, on se focalisera sur le cas
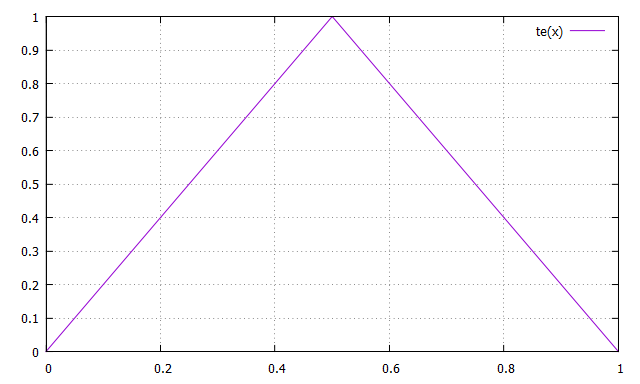
Propriétés de t :
t(0) = t(1) = 0
t(1/2) = 1
t(1/3) = t(2/3) = 2/3 ; 1/3 -> 2/3 -> 1/3...
1/7 -> 2/7 -> 4/7 -> 1/7...
Itération
Tent Map itérée
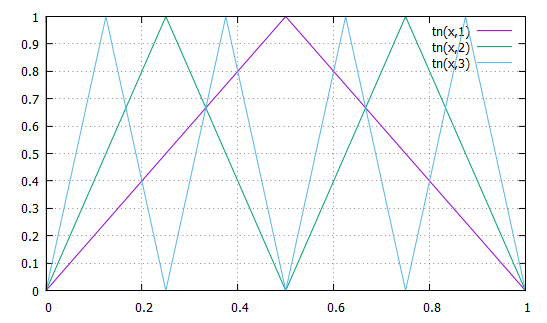
Il est facile de montrer que, ∀x ∈ ℝ et ∀n ∈ ℕ,
La séquence des itérés d'un point
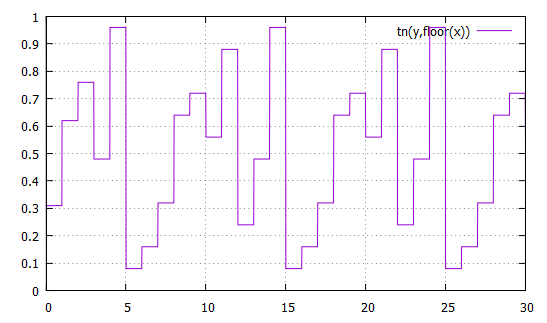
Orbite de 0.31
Séquence de symboles binaires et code Gray
L'idée est que l'on associe à chaque position de l'orbite d'un point
On remarque que
Soit
et par conséquent
On définit alors
# Pour les graphiques gnuplot on définira la somme partielle tn(x), et on prendra T(x) = tn(x,30)
b(x) = (x<1/2)?0: 1
tn(x,n) = (n == 0)?x: t(x*2**(n-1))
bn(x,n) = b(tn(x))
T1(x,n) = (n== 0)?b(x):bn(x,n)*1./2** n+T1(x,n-1)
T(x) = T1(x,30)
On affiche
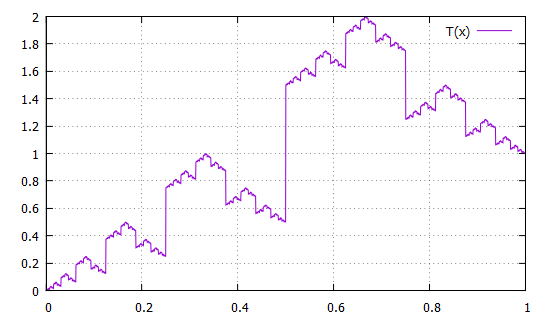
Le graphe de T est identique à celui du code Gray, à l'échelle près...
Rappelons qu'on définit
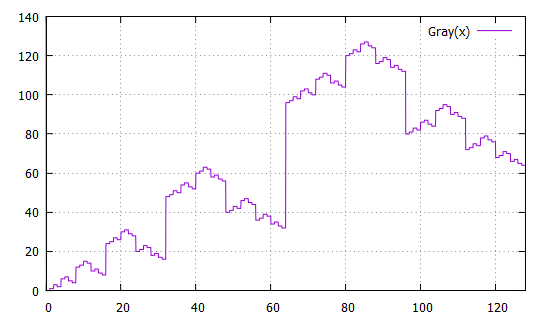
Quelle est l'explication ?
Sommes partielles de symboles.
On va définir
Théorème
Pour
Ainsi,
Sur la figure ci-dessous, on a tracé la courbe
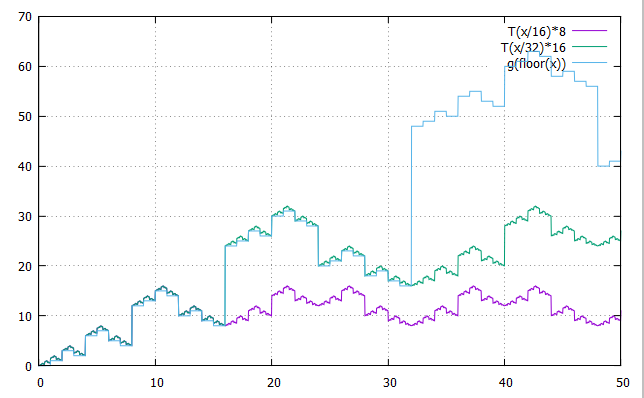
Ce qui est intéressant, c'est que ce théorème fait le lien entre T, qui est une addition de bits, et le code de Gray, qui est un XOR.
sans les symboles...
En fait il n'est pas nécessaire de définir une somme pondérée de symboles ; la somme pondérée des valeurs des itérés successifs de la tent map conduit (presque) au même graphe !
Commentaires (0) :
Page :Ajouter un commentaire (pas besoin de s'enregistrer)
En cliquant sur le bouton "Envoyer" vous acceptez les conditions suivantes : Ne pas poster de message injurieux, obscène ou contraire à la loi, ni de liens vers de tels sites. Respecter la "netiquette", ne pas usurper le pseudo d'une autre personne, respecter les posts faits par les autres. L'auteur du site se réserve le droit de supprimer un ou plusieurs posts à tout moment. Merci !Ah oui : le bbcode et le html genre <br>, <a href=...>, <b>b etc. ne fonctionnent pas dans les commentaires. C'est voulu.