Journal d'un Terrien
Web log de Serge Boisse
On line depuis 1992 !
http://sboisse.free.fr/science/maths/Mes Recherches mathematiques/iteration/l_application logistique.php
Voir aussi: mettre ici des liens entre vers des sujets voisins
Itérations et chaos
Tent map
Is the Logistic Map hiding in the Mandelbrot Set? (video Youtube)
L'application logistique
Sous sa forme le plus générale c'est l'application
La fonction logistique est aussi la dérivée de la fonction sigmoïde
En effet
cf. La fonction sigmoïde et son étonnante dérivée ! (video Youtube)
Itérations de l'aplication logistique
On pose
etc
Graphe de L(x) et de ses deux premières itérations :
En posant
Cela marche aussi pour des k non entiers ! ici
Par contre il y a des problèmes dus à multi valuation des solutions de
On obtient aussi le graphe de
Il s'agit bien sûr de
Séquences de symboles
L'idée est que l'on associe à chaque position de l'orbite d'un point
Soit
Remarquons que
On définit alors
gnuplot
L(x)=4*x*(1-x)
Lk(x,k)=(k<=0)?x:Lk(L(x),k-1)
b(x) = (x<0.5)?0: 1
S1(x,k)=(k<=0)?floor(2*x):b(Lk(x,k))/2.0**k+S1(x,k-1)
plot [0:1] S1(x,20)
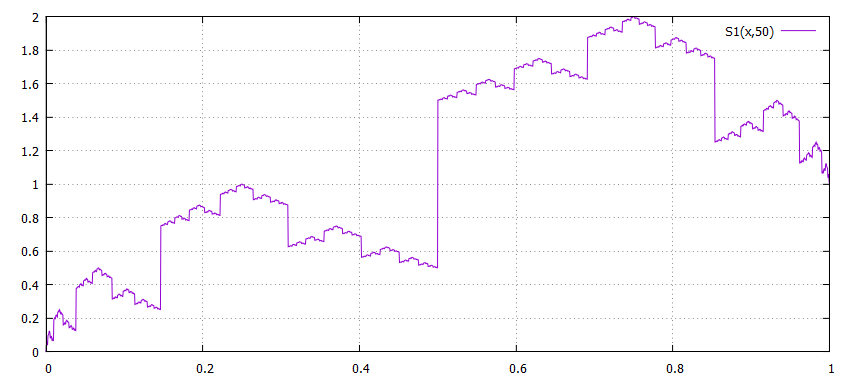
Surprise, le graphe de S1x) est (presque) identique à celui du code Gray,
Pas tout à fait...
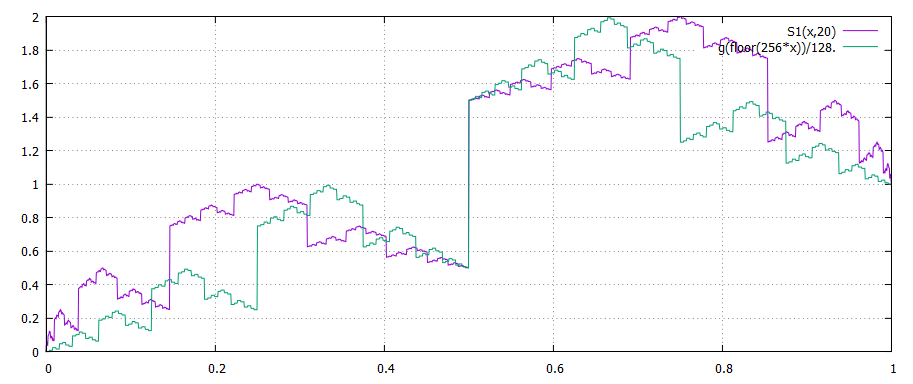
D'où l'idée de regarder ce que donne le code gray inverse ig(x) (aussi appelé Intégrale de parité) de, disons S1 multiplié par 128 :
On obtient, à 0.5 près, un arc sinus !
gnuplot
ig(x) = ig2(0,floor(x))
ig2(r,n) = (n<=0) ? r: ig2(r^n, n/2)
plot [0:1] ig(S1(x,20)*128)/256., asin(2*x-1)/pi
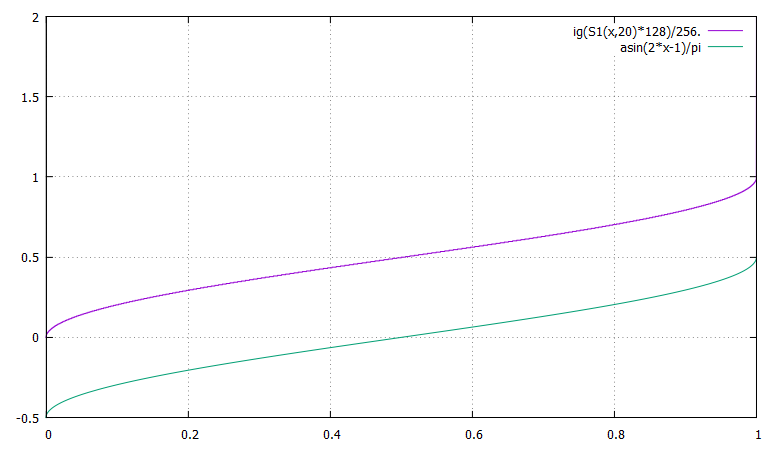
Et donc S1(x,30)*512,g((asin( 2*x-1)/pi+.5)*1024.)
et pour tout k puissance de 2 assez grande, et
S1(x,30)*k = g((asin( 2*x-1)/pi+.5)*2.*k)
L'approximation est déjà très bonne pour n=20 et k=10
On notera que
Application logistique bidimensionnelle
On pose
cf factologsin2+logistique.txt (fichier sur D)(lien privé)
Racine carrée fonctionnelle de l'application logistique
on va considérer si on peut obtenir
Commentaires (0) :
Page :Ajouter un commentaire (pas besoin de s'enregistrer)
En cliquant sur le bouton "Envoyer" vous acceptez les conditions suivantes : Ne pas poster de message injurieux, obscène ou contraire à la loi, ni de liens vers de tels sites. Respecter la "netiquette", ne pas usurper le pseudo d'une autre personne, respecter les posts faits par les autres. L'auteur du site se réserve le droit de supprimer un ou plusieurs posts à tout moment. Merci !Ah oui : le bbcode et le html genre <br>, <a href=...>, <b>b etc. ne fonctionnent pas dans les commentaires. C'est voulu.