Je vous propose ici une extension nouvelle de la composition de fonctions mathématiques (traditionnellement notée ).

Si on note
, et ,etc., alors on va définir ici des choses comme  ou , un  sujet d'étude qui, je crois, est entièrement nouveau !

On s'intéresse ici à des fonctions continues et au moins surjectives d'un domaine D sur un sous-ensemble ou une extension de D, par exemple d'un intervalle réel sur lui même. Par exemple si trois fonctions f, g, h sont (avec les bons domaines de définition, que je ne détaillerai pas ici) telles que :

et

alors on a  et on peut poser par convention 
De même si alors on peut poser par convention 
Plus généralement si alors par définition 

Par exemple il est facile de vérifier que

On a ainsi un moyen de composer "fractionnellement" des fonctions, ou de définir des puissances fractionnaires de composition. Naturellement lorsque "l'exposant" entre crochets est entier, on a la composition de fonction classique avec ses propriétés usuelles, telles que l'associativité et le fait que  identité

La notation  me semble bien meilleure que le  des américains (sans crochets), qui est détestable à cause de la confusion possible avec 1/f. Ainsi on pourrait remplacer les discutables et par  et  sans risque d'erreur.

Il est également possible d'utiliser la notation alternative au lieu de Ainsi

Bien que l'on ait , c'est le seul cas où . 
Ainsi alors que 

Exemple (tiré d'une thèse de Feliks Burdecki, datant de 1926 !) :
Soit
il est facile de voir que et que par conséquent pour p entier positif,

d'où l'on tire notamment que si alors lorsque la limite vaut

il se trouve que cette formule pour est aussi valable pour les fractionnaires !
par exemple si , alors

Autre exemple : soit l'application "logistique" bien connue ,  de l'intervalle [0,1] vers lui-même.
En posant , on a
et plus généralement, pour p entier positif,
mais cela ne marche pas  si p n'est pas entier...

D'une manière générale, trouver  connaissant est un problème assez difficile, trouver  ou  est encore plus ardu !

La composition fractionnaire de fonctions pose des problèmes nouveaux. Par exemple on aimerait bien que, pour toute fonction composable avec elle-même,   soit "proche" de   parce que et sont des réduites successives de en fraction continue. Peux-t-on définir cette proximité, et cette conjecture est-elle vraie ?

Autre conjecture :
lorsque , et pour toute fonction continue de D sur D, é ?

Enfin, peut-on définir des choses comme  ou ? (Une composition imaginaire de fonctions !) Je serais intéressé par une expression de  ou !

Tous ces problèmes sont ouverts. Mathématiciens, à vous de jouer !

Je suis tombé sur un intéressant article de wiképédia, iterated function (en anglais). Il apparaît que l'idée d'itération fractionnaire n'est pas nouvelle (Zut, moi qui croyais l'avoir inventé...) et qu'elle est reliée à la notion mathématique de flot.

Par ailleurs plusieurs personnes ont cherché une solution à . On peut trouver un résumé de ces recherches ici.  Il apparaît que la solution n'est pas unique, mais que si l'on s'intéresse aux x réels positifs,  alors elle a une croissance plus rapide que tout polynôme tout en étant moins rapide que toute exponentielle. C'est donc une nouvelle classe de complexité (ou croissance). C'est intéressant.

Je me suis toujours demandé si l'on ne peut pas faire un parallèle entre les les classes de croissance de fonctions et les ordinaux.  Par exemple si les polynômes P sont associés à l'ordinal P(ω), et si exp est associé à l'ordinal , qu'y a-t-il entre deux ? Cette question me fascine.

Etant donné une fonction bijective d'une partie D de ℝ ou ℂ dans elle-même, et un entier , on notera la composée de f par elle même.

Par exemple , et est la réciproque de , généralement notée abusivement (mais pas dans ce texte) .😒

Ne pas confondre , la composée de par elle-même, et , le carré de . Ainsi, est le carré de la composée, et est la composée du carré.

On a bien sûr :

On va explorer ici le cas où n'est pas entier. Dans ce qui suit sera donc un réel.

C'est un exemple très connu. Soit la fonction de [0..1] dans [0..1] définie par :

En posant , on obtient

et donc

et

La surprise est que cela marche aussi pour k non entier !

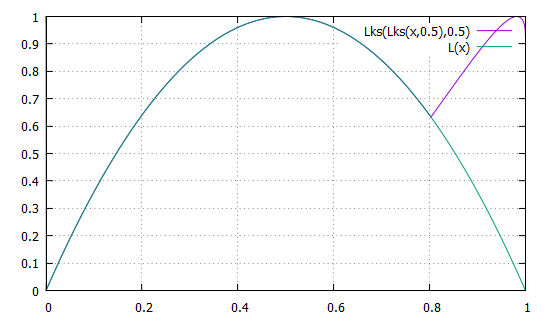
Ainsi

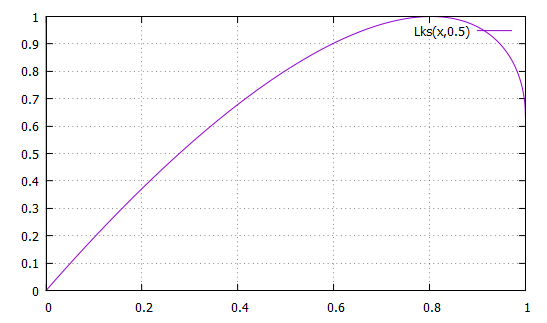
Mais, du fait que Cette application a un maximum en ≃ 0.802..., n'est pas égal à si :

cf Fractional Derivative (vidéo Youtube)

Dans cette vidéo on définit la dérivée fractionnaire comme l'inverse de l'intégrale fractionnaire, elle-même définie à partir de la relation de Cauchy pour les intégrales multiples, en considérant l'intégrale comme une transformée que l'on appellera :
si on pose alors

étant un paramètre qu'on choisit (non localité) on on devrait écrire
et donc pour n réel positif,

pour n > 0
Et donc on définira

(à nouveau on devrait écrire )

Ce qui permet de définir un opérateur intégro-différentiel (differintegral operator) , qui vaut , , et

On a les propriétés suivantes :

attention la "chain rule" et la "product rule" ne marchent plus...

On peut être tenté de tracer le graphe des itérés successifs d'un réél de départ, c'est à dire tracer le graphe d'une fonction telle que

Cela conduit à se demander s'il peut exister une fonction telle que , pour un donné, et pour tout positif,

Par exemple si , on a , et bien sûr si , on retrouve

Supposons qu'il existe une telle fonction telle que cela soit vrai pour quelconque, alors

Si cette expression admet une limite quand , alors on peut définir la pseudo-dérivée de par composition fractionnaire, que l'on notera , et q'il ne faut pas confondre avec :

Par exemple pour , on a bien sûr et

Ce qui est un résultat intéressant et inattendu. #découverte
J'appelle cela le germe par composition de la fonction . En l'itérant un nombre infini de fois, on retrouve . #TBC

Pour l'application logistique précitée,

et on constate que tend vers une courbe limite quand :

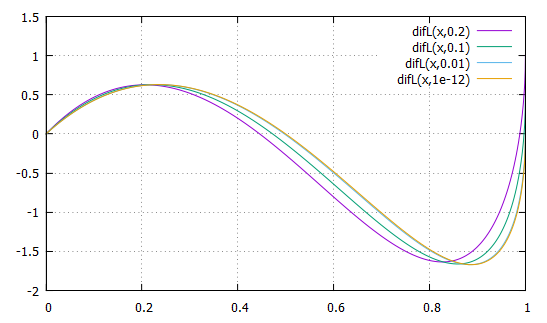
Il est remarquable que cette courbe n'est pas paire alors que L(x) l'est.

Mais il me semble que seule la partie pour a un sens ?

#TBC A suivre...

index de mes pages "maths"