Auteur: Serge Boisse
Date: Le 27/03/2023 à 13:03
Type: web/MOC
Tags: maths,suite,morphogenèse,cosmologie
pub: oui
commentaires: ouiCopier

Un Univers-Graphe

Je vous propose dans ce document de jouer à Dieu, pas moins !
Mettons-nous donc dans la peau de Dieu au moment où il décide de créer l'univers !
Notez que peu importe le moment, vu que Dieu vit hors du temps et que le temps n'existe pas encore !
D'aileurs c'est bien connu, "au commencement il n'y avait rien". Traçons donc une figure pour représenter ça :

Eh, oh , c'est de la triche ! rien , c'est rien ! Ce n'est pas le mot "rien" ni quoi que que ce ce soit d'autre !
Certes, mais qu'est ce qui nous empêche de nommer ce rien ? Au commencement était le Verbe, dit-on aussi, et le pouvoir du Verbe, c'est de nommer ! Après tout, les hommes on aussi inventé le chiffre zéro, et le symbole de l'ensemble vide, pour décire le "rien" ! Qu'est ce qui empêche Dieu de faire la même chose ? ... Rien !

Très bien, alors que fait ce rien ? Et bien naturellement, rien. Vu qu'il n'y a rien d'autre, il ne peut rien faire que de contempler son propre nombril. En clair, Rien ne fait rien. Si je matérialise la relation "faire" ou "contempler" par un arc, alors donc j'obtiens la figure suivante :

Eh, mais c'est encore de la triche ! C'est quoi ce truc !  Où on va, là ?  Mais nulle part, voyons ! Je ne fais que décrire ce qui découle des trois simples évidences (méta règles) suivantes :
1) au commencement il n'y avait rien,
2) lorsqu'il y a quelque chose je peux lui donner un nom, et
3)Un objet peut se contempler lui-même ou un autre objet.
Vous n'allez quand même pas m'interdire ça, non ?

Très bien. Alors nous avons maintenant quelque chose de nouveau : cet arc qui permet au rien de se mettre en relation avec lui-même. Un arc, ce n'est pas rien ! C'est autre chose. Je peut lui donner un nom : disons arc1. Et qu'est ce que j'obtiens ?

Tiens ? me voila avec deux objets... non, quatre objets : "rien", "arc1", l'arc qui va de "rien" vers "arc1" et l'arc qui va de 'arc1 vers "rien". Bon, alors allons-y !

Arrivé ici, je dois faire un choix : est-ce que je continue comme à créer des objets à partir des arcs qui les relient, auquel cas je vais arriver à quelque chose comme :

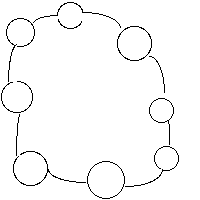
Ce qui n'est pas très intéressant, ou bien est-ce que je me permet des variations comme la possibilité de dire "si A est en relation avec B, et B en relation avec C, alors il existe une relation d'un autre type entre A et C". Oui, qu'est-ce qui m'en empêche ?

Bon, mais si je fais cela, je vais me retrouver avec un graphe où tout est en relation avec tout, ce qui n'est pas très intéressant non plus :

Si je ne veut pas que Dieu succombe à un mortel ennui, il me faut chercher une règle plus intéressante :
Par exemple "je crée un arc à la fois, et non pas plusieurs simultanément" En fait, à une étape donnée, j'ai le choix entre "nommer un des arcs existants" ou "créer un nouvel arc" et il me faut choisir entre quels objets !  Nous voyons donc qu'il y a plusieurs "règle du jeu possible" : nous allons donc tester toutes les règles possibles, et ne garder que celles qui conduisent à des situations intéressantes, c'est à dire  à des choses imprévisibles a priori. Dieu (Toi !) est donc conduit à imaginer des  règles qu'il va appliquer ensuite mécaniquement jusqu'a ce qu'il trouve une règle qui conduise à un "monde" intéressant.

Faisons un premier essai : Je peux dire que je vais à chaque étape, procéder en deux temps :

- T1) je nomme un arc , et pour cela je choisi l'arc le plus ancien. (s'il n'y a pas d'arc, je ne fait rien). pour nommer mon arc, je crée un cercle dans lequel j'écrit un nom, puis Je créé d'abord l'arc issu de l'objet origine (le plus ancien)  et allant vers mon nouvel objet,  puis celui allant vers  l'objet destination.

- T2) je  relie entre eux les deux objets les plus anciens non encore reliés. Plus précisément, je choisit l'objet A le plus ancien, et je relie à A l'objet B le plus ancien non encore relié à A s'il existe , sinon je prend comme origine A le second objet par ordre d'ancienneté, etc. Si tous les objets sont reliés entre eux, je ne fais rien.

En repartant de la figure initiale :Il n'a pas d'arc donc j'applique T2 : les deux objets les plus anciens non encore reliés sont "rien" et "rien" (rien ne m'interdit de relier un objet à lui même si ce n'est déja fait). puis à la seconde étape j'applique T1, donc je nomme un arc (il n'y en a qu'un !) J'obtiens donc la seconde figure :
(on notera que les arcs ont des dates, l'arc 1 est créé avant l'arc2)
Ensuite je considère T2 : l'objet A le plus ancien est "rien". L'objet B le plus ancien non encore relié à A est A lui-même, puisque rien n'est maintenant plus relié directement à lui-même : A la fin de cette étape 2, j'ai donc ;
<- situation à la fin de l'étape 2

Passons donc à l'étape 3 : on applique d'abord T1 : l'arc le plus ancien est l'arc 1, je le développe donc :
On notera que j'ai numéroté 4 et 5 les nouveaux arcs, qui remplacent l'arc 1.
Passons donc à l'étape T2 : l'objet le plus ancien est "rien". Il est relié à tous les autres (et à lui même). Le second objet par ordre d'ancienneté est "arc1" (ou "a1" pour simplier") . il est relié à tous les autres objets, sauf à lui même. Je crée donc un arc entre a1 et lui même :
 <- situation à la fin de l'étape 3. Notez que la symétrie des graphes précédent est rompue.

On peut donc passer à l'étape 4 : voyons donc T1 : l'arc le plus ancien est le 2, je le développe donc :
Pour ce faire j'ai crée les arcs "7" et "8". Ensuite, à l'étape T2, je considère l'objet les plus ancien ("rien") et je je constate qu'il n'est pas relié à a1 qui est donc l'objet le plus ancien de cette liste réduite à un seul élément : je relie donc entre eux rien et a1 :
<- situation à la fin de l'étape 4. Ça devient intéressant, n'est-ce pas ? Ce qu'on obtient n'est pas du tout trivial ! Notez que la symétrie rompue à l'étape précédente est restaurée ici...

Cinquième étape (le jour 5 de notre univers en cours de gestation !). Je nomme l'arc le plus ancien (3), puis je constante que "rien" étant relié à tout, il me faut considérer a2, qui n'est pas relié à lui même,  ce que je fais. On obtient donc directement à la fin de l'étape 5 :
 <- étape 5. Symétrie à nouveau rompue.
Pour la sixième étape, je nommerai l'arc 4, puis je relierai "rien" à lui-même. Etc Etc..

Où on va ?

Nous avons constaté sur cet exemple que l'application de règles simples permet de développer un graphe initialement réduit à "rien" dans des directions intéressantes et non triviales. Je pose donc la question : finalement, est ce que notre univers ne serait pas né comme ça, tout simplement, mine de rien ;-) ?
Réfléchissez-y, je serai ravi de lire vos commentaires !

> La suite : La fonction qui se commente elle-même
< page précédente : Commentaires