Je me suis récemment intéressé à l'utilisation des angles en physique : il me semble qu'une description "angulaire" de la physique pouvait être riche d'enseignements. Par exemple en mécanique quantique, le fait que toutes les descriptions de l'énergie se réduisent en fin de compte a des fonctions périodiques du temps devrait nous conduire à une description géométrique de l'espace-temps où les rotations de l'espace des phases auraient un sens physique.

Mais la meilleure description géométrique de l'espace-temps reste celle de la relativité. Je vous propose donc de revisiter la relativité restreinte et la célèbre transformation de Lorentz d'un point de vue "angulaire".

Commençons par le b-a ba de la relativité restreinte.

Un evénement est un quadruplet (x,y,z,t) de nombres réels, les trois premiers indiquant où, le dernier quand, l'événement s'est produit (pour un observateur O dans un cadre de référence donné). Le même événement pour un observateur O' sera un autre quadruplet( x',y',z',t') qu'il obtiendra en utilisant ses moyens de mesures et ses horloges.
Supposons que l'observateur O', c'est à dire son système de référence, est en déplacement uniforme à à une vitesse v (mesurée par O) dans la direction x. Quelle est la relation entre (x',y',z',t') et (x,y,z,t) ?

En mécanique classique (Newtonienne), les deux quadruplets sont liés par la transformation de gallilée :
t' = t,  y' = y,  z' = z,  x' = x-vt
Toutes les lois de la mécanique classique restent inchangées par cette transformation.

Cependant comme l'a observé Einstein, si un éclair se produit en O à (0,0,0,0) c'est à dire au moment où nous supposons que les deux systèmes sont confondus, le front de l'onde se déplace selon la loi
 où est la vitesse de la lumière

L'observateur O' qui guette la propagation du signal lumineux doit arriver à la même équation dans le système de coordonnée S', parce que les lois de la physique doivent rester invariantes par changement du référentiel (principe de relativité, LE principe fondamental de la physique).
soit :
Ce qui est incompatible avec la transformation de Gallilée.
Quelle est la transformation qui respecte l'équation de l'onde ?

On peut démontrer qu'il existe une solution linéaire, c'est à dire de la forme :

Et on cherche les coefficients

En reportant dans l'équation [2] , on trouve assez facilement :

Ce qui est sous sa forme la plus simple la célèbre transformation de Lorentz, avec deux conséquences remarquables :

L'importance fondamentale des transformations de Lorentz est que toutes les lois de la physique doivent rester invariantes par ces transformations. Bien que cela soit simplement une autre expression du principe de relativité, cet énoncé ramène la physique à la géométrie, plus précisément à l'étude des invariants du groupe de Lorentz (les transformations qui laissent invariante la forme x2+y2+z2-c2t2)

L'analogie est encore plus frappante si l'on se souvient qu'en géométrie plane Euclidienne, les rotations d'un système de coordonnées sont représentées par les matrices

telles que A'A = I, où A' est la transposée de A. On montre que ces matrices doivent avoir la forme

Or la matrice définie par la transformation de Lorentz est

Mais si au lieu de (x,t) et (x',t') nous prenons (x,ict) et (x', ict')   (où i2 = -1), nous obtenons la matrice :

Et il est maintenant possible de trouver un réel alpha tel que

et

 
et notre matrice devient

Que l'on peut interpréter comme une "rotation d'un angle imaginaire" du système de coordonnées (x, ict). N'y voyez aucune signification mystique ! C'est seulement la traduction en français d'une constatation géométrique.

Dans tous les livres de physique, on met en garde le lecteur en lui affirmant "qu'aucune signification physique n'est liée à cette terminologie". Tiens donc ? Il me semble quand à moi que l'on peut en tirer quelque chose.

Par exemple si alpha=0, cela correspond au cas v /c = 0 :
en identifiant cosh(alpha) et ,  on trouve

correspond à
correspond à
De telles vitesses n'ont jamais été atteintes, même avec des faisceaux de particules. Ceci permet donc quelques spéculations :

Supposons que cette rotation imaginaire soit une vraie rotation autour d'un axe imaginaire : un tour complet (alpha = 2pi) correspond à une vitesse de c * sqrt(1-1/ch2(2 pi)) = 0.999993 c ; mais après un tour complet on se retrouve à la position de départ, c'est à dire à la vitesse zéro ; simplement la masse aura augmentée dans la proportion de 1/(1-(v/c)2)1/2, c'est à dire de ch(2pi) = 267.747.

De même après k tours, la masse a augmentée d'un facteur ch(2k pi)

Je pense qu'une particule de  masse au repos m, lancée à la vitesse de c sqrt(1-1/ch2(2k pi)), est indiscernable d'une nouvelle particule immobile dont la masse est m' = mch(2k pi) ; évidemment pour que la position de la particule reste fixe le mouvement doit être un mouvement de rotation (spin).

Ou, si l'on préfère, qu'une particule lancée à la vitesse de c sqrt(1-1/ch2(2k pi)), est indicernable d'une particule de même masse au repos lancée à la vitesse de c sqrt(1-1/ch2(2l pi)), où k et l sont des entiers.

Ce qui est intéressant, c'est le rapport des masses relativistes mesurées : m2/m1 = ch(2k pi) / ch(2l pi).
En effet les mesures de masses sont relatives : on mesure des masses relativement à leurs effets sur d'autres masses. La seule masse "absolue", c'est la masse de Planck  mp = hc/G ~ 10-5 grammes .

Je prétends que le processus décrit correspond à la création de nouvelles particules, qu'il existe une infinité de particules, mais que les seules particules présentes dans l'univers sont celles dont les masses sont mp * ch(2k pi) / ch (2l pi) , avec k et l entiers, l > k

L'espace des phases, c'est un espace abstrait a 6 dimensions dans lequel chaque "point" a 6 coordonnées, trois coordonnées de position px py pz et trois coordonnées de vitesse vx vy vz ; c'est pratique car un seul point de l'espace des phases donne tous les renseignements sur le déplacement d'une particule.

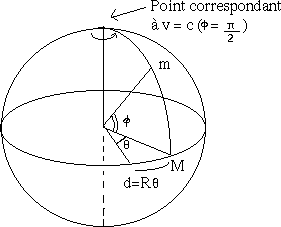Limitons nous à une coordonnée d'espace x et une coordonnée de vitesse v ; l'espace des phases de la relativité restreinte est courbe. Nous ajoutons donc une troisième dimension pour visualiser la courbure (rayon de courbure R). La position sera repérée par le marqueur thêta et la vitesse par le marqueur phi.

Pour un observateur immobile le déplacement d'un objet à la vitesse v sera d=Rtheta et la vitesse sera reliée à l'angle phi par la relation v = c sin(phi). Pour cet observateur, les photons cercleront autour des pôles en suivant des trajectoires de longueur nulle.

Soit M1M2 un déplacement perçu par un observateur au repos. Dans l'espace des phases le déplacement réel correspond à l'arc (m1 m2) qui se projette selon l'arc (n1 n2) dans le plan équatorial. Le segment [O n1] = Rcos phi. L'arc (n1 n2) = [O n1] theta. Comme  cos2 phi + sin2 phi = 1 et sin phi = v/c, on a :

(m1 m2) = (M1 M2) , qui n'est autre que la contraction de Lorentz.

Dans l'espace des phases le temps n'est pas une variable libre. Le temps propre se calcule. Il est proportionnel à l'arc (T1, T2), projection de l'arc (m1 m2) sur le plan tangent au pôle :

t = (T1 T2) / c = thêta R cotg(theta) / c

Nous avons donc deux points de vue sur la transformation de Lorentz :
Dans le premier, on a une rotation d'un angle imaginaire i alpha du système de coordonnées (x,ict) de l'espace réél.
Dans le second, on a une rotation d'un angle réel phi du système (x,v) de l'espace des phases

Dans le premier cas,  = 1/ch(alpha)
Dans le second cas,  = cos (phi), puisque v/c = sin(phi) par définition de phi.

d'où

soit

Ou encore après quelques transformations, en utilisant arg ch(x) = log(x+sqrt(x-1)) :

  alpha = log(1/cos(phi)+tan(phi))  = log( (1+sin(phi)) / cos(phi) )  [6]

On remarquera que l'équation [6] n'a de solutions réelles que si 1/cos(phi) >1, puisque arg ch(x) n'est défini que pour x > 1, c'est a dire - pi/2 <=  phi <= pi/2 ; mais c'est bien le cas ici, puisque on suppose qu'on ne peux pas dépasser la vitesse de la lumière.

alpha = 2pi pour phi = 1.567 et sin(phi) = 0.999993, que nous retrouvons donc.
alpha = pi pour phi = 1.48442 et sin(phi) = 0.996272 => v = 298675 km/s

Si alpha a vraiment un sens "angulaire", à cette vitesse une particule devrait "s'inverser", i.e. se comporter comme une antiparticule. Or on n'observe pas cela.

Objection retenue.

> La suite : La relativité