Auteur: Serge Boisse
Date: Le 27/03/2023 à 19:03
Type: web/MOC
Tags: physique,relativité,quantique,psychologie
pub: oui
commentaires: ouiCopier

Quelques réflexions sur le théorème du libre-arbitre

Le théorème du libre-arbitre prouve que si nous avons un libre-arbitre (dans un sens très précis), alors les particules élémentaires aussi ! J'ai longuement réfléchi sur ce théorème, et je suis arrivé à la conclusion qu'il pourrait être faux  si  une certaine hypothèse, implicitement admise par Conway, était fausse : celle que l'information ne peut pas remonter le temps ! En d'autre termes, Conway  a peut-être tort ! 

Le théorème

Mais commençons par le commencement : le théorème du Libre-arbitre, démontré par John Conway et Simon Kochen  en 2006.

Le théorème se base sur l'idée que deux expérimentateurs humains séparés par une certaine distance (disons dans deux labos éloignés l'un de l'autre) vont procéder à des mesures sur des particules atomiques, et utiliser leur libre-arbitre pour choisir, au dernier moment, quelle mesure ils vont faire.  Plus précisément, ils vont effectuer chacun des mesures de spin sur une particule élémentaire, mais ces deux particules seront "intriquées" (nous verront plus loin ce que cela veut dire). Les deux expérimentateurs vont faire ces mesures quasi simultanément, de telle sorte que chaque expérimentateur n'a pas la possibilité de transmettre l'information "quelle mesure je vais faire" à l'autre avant que ce dernier n'ait enregistré le résultat de sa mesure.

Ce théorème repose sur trois axiomes que Conway nomme "Fin", "Spin" et "Twin" (si ces axiomes ressemblent à du chinois pour vous, continuez quand même à lire, je vous explique ça en clair un peu plus bas !

1. "Fin" : Il existe une vitesse maximale de transmission de l'information.   Autrement dit, l'information ne peut être transmise qu'à vitesse finie et il existe une borne supérieure à cette vitesse. 
2. "Spin" : le carré des composante de spin  de certaines particules de spin 1, mesuré dans trois directions orthogonale, est toujours une permutation de (1,1,0). J'expliquerai plus loin ce que cela signifie, mais on peut déjà dire que ce résultat a été prouvé expérimentalement
3. "Twin" : Il est possible "d'intriquer" deux particules élémentaires et de les séparer spatialement ensuite,  de telle manière que si on mesure ensuite leur spin selon deux directions parallèles, les carrés des deux composantes de spin sont  égales.  J'expliquerai également plus loin ce que cela signifie, mais on peut déjà dire que ce résultat a été lui aussi prouvé expérimentalement (pour les particules de spin 1/2 jusqu'à 10 Km de distance)

Ces trois axiomes sont parfaitement "raisonnables"  au sens ou les physiciens quantiques les considèrent comme vrais tous les trois. En particulier si "Spin" ou "Twin" étaient faux les fondements même de la mécanique quantique seraient ébranlés.

Le théorème dit alors que si deux expérimentateurs sont libres de choisir quelles mesures ils vont faire (c'est à dire selon quels axes ils vont mesurer les spins), alors le résultat des mesures ne peut être déterminé par aucune fonction mathématique dont les arguments seraient des états de l'univers antérieur à ce choix.

Définissons le "Libre-arbitre de Conway" comme suit : Une entité dispose de libre arbitre (au sens de Conway) à l'instant t si son état ne peut pas être décrit comme résultat de l'application d'une fonction, au sens mathématique du terme, portant sur l'information accessible par cette entité, c'est à dire l'ensemble des évènements qui se trouvent dans le "cône de lumière passée" de cette entité. En particulier le "libre arbitre de Conway" d'un expérimentateur peut le conduire à choisir l'axe sur lequel il va effectuer une mesure de spin.

Le théorème dit alors que si les expérimentateurs disposent du libre-arbitre (de Conway), alors les particules aussi !

Pourquoi ce théorème s'appelle-t-il le "théorème du libre-arbitre" ? Les philosophes considèrent généralement que les expérimentateurs ont assez de "libre arbitre" pour choisir la manière dont ils organisent leurs expériences d'une manière qui n'est pas déterminée par l'histoire passée. Le théorème en déduit le fait surprenant que si cela est vrai la réponse des particules n'est pas non plus déterminée par l'histoire passée !

Évidemment ce "libre arbitre de Conway" diffère notablement de ce que les philosophes appellent "libre-arbitre",  mais si on réfléchit, la définition de Conway est nettement plus opérationnelle, et moi, je la préfère ! Attention, Conway et Kochen ne prouvent pas que l'univers est indéterministe (ni déterministe, d'ailleurs).  Il ne faut pas  faire dire au théorème plus qu'il ne dit !

Dire qu'une particule possède un libre-arbitre de Conway, c'est dire que son état est indéterminé à l'instant t, mais son spin n'est pas pour autant libre de prendre n'importe quelle valeur lors de la mesure (par exemple les mesures sont contraintes par l'axiome "Spin"), et donc ces mesures ne sont pas aléatoires. Il semble exister quelque chose entre "indéterminé" et "aléatoire", et cela pose quelques questions intéressantes.... Mais ce n'est pas l'objet de cet article !

Les axiomes

Expliquons un peu les trois axiomes :

L'idée que l'on ne peut transmettre de l'information à une vitesse infinie est naturelle, et elle constitue même l'un des piliers de la relativité restreinte. Mais l'axiome "Fin" (prononcer : "fine") ne suppose pas nécessairement cette vitesse limite est la vitesse de la lumière. Il suppose seulement qu'il y a une limite finie.

En fait pour bien comprendre l'axiome il faut aller un peu plus loin car les choses ne sont pas si simple. En relativité restreinte, tout est évènement, et le "choix" d'un expérimentateur de la mesure qu'il va faire est un évènement, de même que la mesure par un appareil du spin d'une particule est un autre évènement.  Un évènement est donc un "point de l'espace-temps", quelque chose qui est décrit par quatre coordonnées x,y,z et t.

Mais en relativité, l'ordre temporel de deux évènements a et b peut être distinct selon le cadre de référence que l'on choisit pour les coordonnées.  Si l'on choisit deux cadres en mouvement l'un par rapport à l'autre, a peut précéder b dans l'un des référentiels, et b peut précéder a dans l'autre !  Quel sens cela a-t-il alors de dire qu'un évènement a ne peut pas influencer causalement un évènement b ?  En fait, si une information est réellement transmise de a vers b, alors elle le sera quelque soit le cadre de référence choisi pour les coordonnées. Conway propose de dire alors que l'information est "effectivement transmise" de a vers b.

Et l'axiome "Fin" se formule en fait précisément ainsi : Il existe une borne supérieure finie à la vitesse à laquelle une information peut être effectivement transmise.

Contrairement à "Spin" et "Twin", cet axiome ne peut pas être vérifié expérimentalement.  Il faut donc l'admettre, mais il faut dire qu'il est cohérent avec le principe de causalité selon lequel les effets ne peuvent précéder les causes, et qu'il est cohérent aussi avec la relativité restreinte.

Le spin est une propriété des particules subatomiques, qui ressemble un peu au moment cinétique de rotation des objets à notre échelle.  Mais comme toutes les notions quantiques, le spin est une notion très bizarre. On ne peut pas dire qu'une particule élémentaire tourne sur elle-même. Cela n'a pas de sens. Pourtant elle possède  un "spin", comme elle possède une masse ou une charge. Mais on ne peut pas déterminer son "axe de rotation", cette notion même n'a pas de sens. On peut seulement mesurer la composante de son spin selon un axe (une direction) que l'on choisit à l'avance, et le résultat de cette mesure est toujours quantifié, c'est à dire qu'en choisissant les bonnes unités, ce sera toujours un nombre entier.  Pour une particule dite "de spin s", où s est un nombre entier, le résultat de la mesure du spin selon un axe (la projection du spin sur cet axe, si l'on veut, tout en sachant que cette image est fausse), sera toujours un nombre entier compris entre -s et +s. Ça peut paraître bizarre, mais c'est comme ça que le monde est fait selon la théorie quantique. Dans le théorème du libre-arbitre, on considère des particules de spin 1 (par exemple un noyau d'hélium), et donc pour ces particules toute mesure du spin selon un axe quelconque renvoie l'une des trois valeur -1, 0 ou +1, et ceci quelque soit l'appareillage utilisé pour la mesure (je ne détaille pas ici, mais on mesure en fait des champs magnétiques, dont on déduit le spin).

Dans l'axiome "Spin", on considère les mesure de spin d'une particule de spin 1 selon trois axes orthogonaux,  et on considère le carré des résultats de mesure, qui valent donc toujours 0 ou 1. L'axiome dit que la somme de ces carrés est 2, c'est à dire qu'on y trouvera toujours deux "1" et un zéro, ou encore que les carrés des trois mesures  sont toujours (1,1,0) ou (1,0,1) ou (0,1,1) . Cela fait très longtemps que les expérimentateurs font des mesure de spin sur les particules, et les résultats sont toujours conforme à l'axiome "Spin", qui est donc naturel.

En mécanique quantique, on dit que deux particules sont "intriquées", ou "jumelles", lorsqu'elles ont interagi entre elles de telles façon qu'à l'issue de leur interaction,  et même si elles sont séparées ensuite, les deux particules renvoient les mêmes "réponses" aux mêmes "questions". C'est à dire que si l'on mesure le spin de l'une des deux particules selon la direction w, et que l'on mesure le spin de l'autre particule selon un axe parallèle à w, les deux mesures seront identiques. C'est ce que dit l'axiome "Twin". Plus précisément il dit que si l'on  effectue sur l'une des particule trois mesures selon trois axes orthogonaux, et que les carrés des trois mesures sont i,j,k, alors si l'on effectue une seule mesure sur la particule jumelle selon un axe qui se trouve être parallèle à l'un de ceux utilisés pour les mesures sur la première particule, alors le carré du résultat est bien le même (c'est à dire i,j, ou k selon le cas) que celui que l'on avait trouvé sur la première particule pour l'axe parallèle.

Les physiciens savent depuis quelques années comme préparer des particules intriquées, et continuent leurs recherches sur ces objets (ou couples d'objets ?) fascinants parce qu'on peut réellement les considérer comme une seule particule !

Nous allons maintenant décrire la preuve de Conway et Kochen :

La preuve

On va commencer par une petite constatation géométrique : si l'on étiquette par "0" ou "1" chacun des 66 axes de la figure ci-dessus, (elle s'appelle la figure de Peres), il y a un moins un triplet d'axe orthogonaux qui ne peut pas être étiqueté  par (1,0,1)  ou (1,1,0) ou (0,1,1).

En fait, si vous essayez de placer des 0 et des 1 sur les axes de la figure en respectant la contrainte que dans tout triplet d'axe orthogonaux il doit y avoir obligatoirement deux 1 et un 0, vous vous apercevrez que vous n'y arriverez pas, parce que c'est impossible ! Ce n'est pas si simple que ça à démontrer mais c'est simplement une histoire de propagation de contrainte, je ne vais pas vous détailler la démonstration ici. Pour le lecteur intéressé, c'est ce qu'on appelle le paradoxe de Kochen-Specker pour la figure de Peres.  

En fait, je vous ai mis la figure ci contre parce qu'elle est jolie, mais on peut aussi décrire cette figure , qui comporte 16 triplets d'axes orthogonaux, comme suit :

Les axes sont issus du centre d'un cube, et joignent ce centre aux 12 milieux des arêtes, et aux 6x9 points de 6 réseaux réguliers de 3x3 points, chacun étant inscrit dans un cercle lui-même inscrit dans les faces du cubes

Supposons maintenant que le carré de la mesure du spin existe avant la mesure, et donc qu'il existe juste avant cette mesure une fonction S(w) qui donne le spin (le carré de la mesure de la composante du spin en fait) dans la direction w,  S(w) prenant ses arguments sur les directions w issues du centre de la sphère unité. Si cette hypothèse est vraie, et si l'axiome Spin est vrai, pour chaque triplet de directions orthogonales, les valeurs de S seront 1,1,0, dans un certain ordre. Et donc pour pour toute direction -w opposée à w, S(w)=s(-w), et de plus on ne pourra pas trouver  S(x)=S(y)=0 pour deux directions orthogonales quelconques x et y (c'est facile à montrer, essayez !).

Mais comme  au moins un triplet d'axes orthogonaux de la figure de Peres ne peut pas être étiqueté (1,1,0), en réalité notre hypothèse est fausse et donc il n'existe pas de fonction S(w) qui respecte l'axiome Spin. Ceci signifie que la quantité qui est supposée être mesurée n'existe en fait pas juste avant la mesure ! C'est un coup terrible porté à la conception "réaliste" de l'univers. On pourrait donc supposer que cette quantité est instantanément "calculée" à partir de l'information disponible dans l'univers juste avant la mesure. Mais justement le théorème dit que ce n'est pas le cas ! Voyons cela.

Il est possible de concevoir un appareillage compliqué qui permette à un expérimentateur de choisir au dernier moment la direction selon laquelle il va mesurer le spin d'une particule : par exemple l'expérimentateur peut disposer d'une batterie de mesureurs tous orientés selon différents axes, et un "aiguillage" électromagnétique très rapide qui enverra la particule vers l'un des mesureurs.

Maintenant, il faut imaginer deux expérimentateurs que nous nommerons Alain et Barnabé. Alain va choisir de mesurer les (le carré des) composantes de spin d'une particule de spin 1 selon un triplet d'axes x,y,z orthogonaux, qu'il choisira au dernier moment, et que l'on identifiera à l'un quelconque des triplets orthogonaux de la figure de Peres, et Barnabé, qui est dans un laboratoire éloigné, va effectuer la mesure du spin d'une particule  jumelle (intriquée) de celle qu'étudie Alain.  Barnabé va choisir également au dernier moment la direction dans laquelle il va mesurer le spin, en choisissant l'un quelconque des 66 axes de cette figure; En fait, comme S(w)=s(-w) pour toute direction w, Barnabé a le choix entre 33 directions.

Dans le paragraphe précédant, "Au dernier moment" signifie "avant que quoi que ce soit dans le labo d'Alain ait pu  envoyer une indication sur le triplet d'axe qu'il va étudier vers le labo de Barnabé, et inversement". C'est à dire avant qu'un signal quelconque provenant du labo d'Alain ait pu atteindre celui de Barnabé, et réciproquement. S'il existe une vitesse maximale vi de propagation de cette information (ce que dit l'axiome Fin), les deux labos pourront par exemple être éloignés de plus de dt x vi, où dt est le temps écoulé entre le moment où un expérimentateur choisit (par son libre-arbitre !) les axes de mesure, et le moment où la mesure est terminée.

Nous pouvons maintenant prouver le théorème.  Rappelons que celui-ci énonce que le résultat des mesures ne peut être déterminé par aucune fonction mathématique dont les arguments seraient des états de l'univers antérieur à ce choix, et "antérieur" signifie "antérieur dans tous les cadres de référence".

Supposons donc le contraire, c'est à dire affirmons l'hypothèse H que les trois résultats des mesures de spin d'Alain sur ses trois axes x,y,z soient "calculés au dernier moment", c'est à dire que ce triplet de mesures soit la valeur d'une fonction mathématique F dont les arguments sont un ensemble EA d'informations sur des d'évènements antérieurs à la mesure dans un certain cadre de référence inertiel, et bien sûr le choix des axes décidés par (le libre-arbitre de) l'expérimentateur :

F(EA,x,y,z) = (1,1,0) ou (1,0,1) ou (0,1,1)

De même pour la mesure de Barnabé selon la direction w, que l'on doit supposer être calculée à partir de l'information EB disponible dans le "cône passé" de Barnabé (ou plus exactement de la particule qu'il étudie) ; on peut donc écrire :

G(EB,w) =  m, avec m = 0 ou 1

Maintenant si Alain et Barnabé disposent du libre-arbitre au sens de Conway, Alain peut choisir n'importe quel triplet d'axe de la figure de Peres, et Barnabé n'importe lequel des 66 axes de cette figure. Par conséquent EA est indépendant de x,y, et z, et de même EB est indépendant de  w. Mais EA est aussi indépendant de w, car il existe des cadres de référence dans lesquels l'expérience de Barnabé a lieu après celle d'Alain. De même  EB est indépendant de x,y,et z. On peut donc "fixer les directions", c'est à dire que pour tout quadruplet (x,y,z,w) de directions il existe une fonction Fxyz telle que le triplet de résultats enregistrés par Alain soit Fxyz(EA) et une fonction Gw telle que le résultat de Barnabé soit Gw(EB).

En particulier, comme cette fonction Gw renvoie toujours 0 ou 1, elle est un "étiquetage" des 66 directions par 0 ou 1.

Mais l'axiome Twin dit que si Barnabé choisit une direction w parallèle à x,y ou z, alors le résultat de sa mesure sera le même que celui de la mesure d'Alain pour le même axe (c'est à dire l'axe parallèle). Par exemple si Barnabé choisit un axe w parallèle à y, la seconde composante de Fxyz(EA) sera m, c'est à dire  Gw(EB) . Donc,  Fxyz est un étiquetage par 1,0,1 (dans n'importe quel ordre) de tous les triplets d'axe orthogonaux. Ce qui est impossible d'après le paradoxe géométrique de Kochen-Specker  que nous avons vu au début de la démonstration.

Donc l'hypothèse H est fausse et donc les particules disposent du libre-arbitre au sens de Conway !

Il se pourrait néanmoins que la "réponse" d'une particule (disons celle étudiée par Alain) dépendent d'une information E  qui soit disponible après que les axes aient été choisis par l'expérimentateur. Si cette information E dépend d'une information disponible  avant le choix, il n'y a pas de problème, nous sommes dans le cadre discuté ci dessus. Sinon, il existe un instant t0, postérieur au moment où les axes sont choisis, tel que l'information apparaisse spontanément, sans être déterminée par aucune autre information (une sorte d'anti trou noir, on dirait ?). Pourquoi pas, mais dans ce cas le théorème est toujours valide puisque le résultat de la mesure ne dépend toujours pas de l'état de l'univers avant la décision de l'expérimentateur.

Conséquence du théorème du libre-arbitre

Nous avons déjà donné une interprétation du théorème : avec juste l'axiome Spin, on peut déjà prouver qu'un résultat de mesure peut ne pas préexister avant la mesure.  On est donc conduit à supposer qu'il est instantanément "calculé" à partir de l'information disponible dans l'univers juste avant la mesure. Mais justement le théorème dit que ce n'est pas le cas !

Le théorème porte un coup fatal aux théories dites "à variables cachées" (par exemple celle de David Bohm), qui supposent qu'il existe une once de réalité, et que les particules ont plus de propriétés que la mécanique quantique ne veut leur attribuer, mais que ces propriétés sont "cachées", et ne se manifestent que lors de la "réduction du paquet d'onde" qui suit une mesure.  En fait le théorème du libre-arbitre prouve que les théories à variables cachées sont toutes fausses (ou inconsistantes avec la relativité restreinte), et ce sans utiliser la mécanique quantique, puisqu'il s'agit d'un simple raisonnement  mathématique qui n'utilise aucune propriété physique des particules.

Depuis Descartes, les déterministes ont toujours pensé qu'il serait un jour possible de décrire l'univers comme l'évolution d'un système à partir d'un état initial et selon des lois déterministes, c'est à dire qui ne changent pas dans l'espace et le temps. Le raisonnement suivi dans la démonstration ci dessus montre pourtant, sans même utiliser le libre-arbitre mais seulement les trois axiomes Fin, Twin, Spin, qu'aucune théorie qui utiliserait des lois indépendantes de l'espace et du temps ne peut prédire ne serait-ce que le résultat de certaines mesures de spin sur des particules intriquées comme celles d'Alain et Barnabé ci- dessus.

Cependant il se pourrait que le libre-arbitre des expérimentateurs n'existe tout simplement pas. Dans ce cas le théorème ne s'applique pas, et l'univers serait entièrement déterministe, y compris (et surtout !) les actions des humains.  C'est une possibilité logique. En fait, nous avons :

Si les expérimentateurs disposent du libre arbitre (au sens de Conway) alors les particules aussi.

Sinon, cela veut dire que les actions des expérimentateurs sont toujours prévisibles et déterminées ; s'il existe alors une once de libre-arbitre dans cet univers là, ce non-déterminisme ne  s'applique pas aux humains ! ce la semble une position philosophique difficile à tenir, sauf dans le cas d'un solipsisme absolu.

Remarquons encore que le "libre-arbitre" peut se décliner en deux versions : le non-déterminisme et le hasard. On pourrait imaginer que les décisions des expérimentateurs, aussi bien que celles des particules, soient entièrement aléatoires. Mais il faut remarquer que l'existence (vérifiée) des particules jumelles (intriquées) contredit cet argument : si les décisions des particules étaient aléatoires, elles ne pourraient être intriquées. En d'autre termes la liberté peut se jumeler, l'aléatoirité non.  Ce sont deux notions distinctes.

Ma petite contribution

l'axiome Fin est probablement l'axiome le plus subtil des trois. Rappelons qu'il suppose qu'il existe une borne supérieure finie à la vitesse à laquelle une information peut être effectivement transmise, où "effectivement" signifie que l'information est transmise quelque soit le cadre de référence, c'est à dire le système de coordonnées choisi.

En relativité, on modélise le passé et l'avenir d'un objet A par son "cône de lumière". Les frontières de ce cône correspondent à un déplacement à la vitesse maximale, classiquement la vitesse de la lumière, mais on peut imaginer qu'il s'agisse de la vitesse maximale de transmission de l'information, qui est (peut-être ?) différente.   L'axiome Fin dit que seuls les informations disponibles dans le demi-cône inférieur peuvent être connues de A. En d'autre terme l'évènement C ne peut en aucun cas influencer A, parce qu'il est trop loin dans l'espace et pas assez loin dans le passé pour qu'un signal puisse être transmis de C vers A.

De même A ne peut pas influencer l'évènement D, mais il peut influencer l'évènement B qui est dans son futur accessible.

Mais les lois de la physique quantique (de même que celles de la relativité) sont symétriques par rapport au temps.

Par conséquent, il se pourrait qu'il existe une vitesse maximale de l'information (comme le dit l'axiome Fin), mais que cette limite interdise à D et C d'influencer A, mais pas à B d'influencer A !
Double cône de lumière

C'est à dire qu'il se pourrait qu'un évènement futur (tant qu'il reste dans le cône de lumière)  puisse influencer un évènement présent. Dans ce cas le comportement de deux particules A et B, intriquées et séparées dans l'espace, pourrait être  influencé par un évènement C situé dans la partie  commune de leurs deux cône de lumière futur. Autant que je sache, cela reste une possibilité logique.

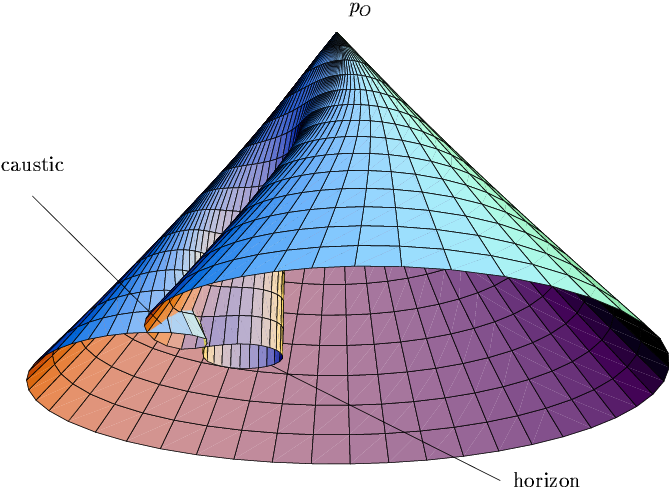
En outre,  en relativité générale, en présence de phénomènes gravitationnels tels que les trous noirs, ou à proximité immédiate des particules, les "cônes" de lumière peuvent se retrouver passablement déformés.

Dans un "cône" de lumière passé tel que celui de la figure ci-contre, certains évènements passés restent inaccessibles à l'observateur bien que leur "horizon" soit dans le cône.  Ce pourrait-il que ce soit dans ces régions inaccessibles que les variables cachées de la physique quantique de Bohm se trouvent ? Cela ne me semble pas être contredit par le théorème du libre-arbitre !

Décidément, la physique quantique n'a pas fini de nous surprendre.