Auteur: Serge Boisse
Date: Le 27/03/2023 à 13:03
Type: web/MOC
Tags: maths,nombre,premier,spirale
pub: oui
commentaires: ouiCopier

La spirale des nombres premiers

A strange discovery about primes numbers

In this page, you can click on any image to view an enlarged version

I present in this page the result of personal researchs I've not been able to see any counterpart in the math litterarture. I present this researchs on graphical form, with severa images. The first five images do not lead to any new or unknown discovery, but the last ones...are very astonishing.

By the way, Renaud Lifchitz discovered the same thing. See his page

1) The facts

Recently, I wanted to plot all numbers "in spiral", that is for every integer n, I plot a point in polar coordinates $(r,\theta )$ with

r = n, and

$theta=n\mathrm{mod}2\pi =n-2\pi [n/2\pi ]$

where the brackets means "take the integer part".

So for instance the 1st numbers are :

n   r   $\theta$ (radians)
1   1   1
2   2   2
3   3   3
4   4   4
5   5   5
6   6   6
7   7   0.716815
8   8   1.716815

For my amusement, I marked the prime numbers on the plot. This gave this plot :(click on image to view an enlarged version) 
Fig 1. Numbers up to 50 are in red, primes are in blue. Circle of radius 10 is in green.

The spirals formation is not ashtonishing : after all, each time you add one to n, you add one to the radius r and one radian to theta (about 57.29 degrees). So when you add 6 to n, you add 6 radians to theta, which is 2pi - 0.283 radians or 16.23 degrees, so a small angle ;  hence the six righthand spirals in which numbers go from six to six.

What is more curious, but can be easily explained, is the fact that prime numbers belong all to TWO of these six spirals, the one starting with 5 (5,11,17...) and the one starting with 1 (1,7,13, 19...). This is because all primes are of the form 6k+1 or 6k+5, just because

• all 6k+0 are divisible by 6
• all 6k+2 are divisible by 2
• all 6k+3 are divisble by 3
• all 6k+4 are divisble by 2

This is elementary. But let us continue a bit, plotting integers from 1 to 200 (click on image to view an enlarged version)
(click on image to view an enlarged version)
Fig 2. Primes up to 200 are big red dots. Other integers are blue points. circle of radius 50 is in green.

We continue to see our righthand spirals, and we just remark that there are holes in the two prime spirals. Again, this is elementary : not all 6k+1 and 6k+5 are primes !

So let us plot integers from 1 to 1000:
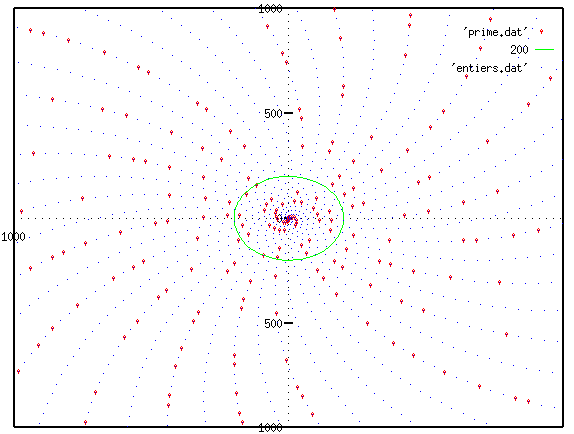(click on image to view an enlarged version)
Fig 3. Primes up to 200 are big red dots. Other integers are blue points

Here, the suprising fact is that we see 44 new, lefthand,  spirals, in which primes belong to 20 spirals only ! Where are our 6 previous righthand spirals ? They are still there ! but our eye tries to see the most 'prominent' figure, which is the 44 spirals.

This number of 44 is one of the "convergent" of the reduced fraction for 2pi :
You may know from your college years that pi can be approximated with 22/7, so 2pi ~ 44/7.  This is the best 3 digits approximation.
You obtain these numbers like this :

2pi = 6.283185307179586... = 6 + 0.283185307179586...  best one-digit approx
2pi ~ 6
1/0.283185307... = 3.531256652... = 3 + 0.531256652... 
2pi ~ 6 + 1/3 = 19/3
1/0.531256652... = 1.882329368... = 1 + 0.882329368...
2pi ~ 6 + 1/(3 + 1/1) = 25/4
1/0.882329368... = 1.133363612... = 1 + 0.133363612...
2pi ~ 6 + 1/(3 + 1/(1+1/1)) = 44/7  : best 3 digit approx
1/0.133363612... = 7.498297203... = 7 + 0.498297203...
2pi ~ 6 + 1/(3 + 1/(1+1/(1+1/7))) = 333/53
1/0.498297203... = 2.006834462... = 2 + 0.006834462...
2pi ~ 6 + 1/(3 + 1/(1+1/(1+1/(7+1/2)))) = 710/113  : best 6 digits approx
1/0.006834462... = 146.3172953... = 146 + 0.31729537598442...
2pi ~ 6 + 1/(3 + 1/(1+1/(1+1/(7+1/(2+1/146))))) = 103993/16551
and so on.

Again, it's an easy task to see that on those 44 new spirals, in each of which integers are of the form n0+44k, with n0 ranging from 1 to 44, only 20 can hold primes (for instance 44k+1 can be prime, but 44k+2 is always divisible by 2, 44k+4 is always divisible by 4 and so forth).

If we look carrefully the above table, we might ask why we do not see 19, 25, 333, 710 spirals ? The answer is : theses spirals are here ! but again our eye see only the most "visible" thing : look again at the plot 1-200, you will see 25 spirals about n~200 : but these are vanishing quickly (in our eyes and minf ly, because the approximation 44/7 is so much more precise.

So let us plot integer between 1 and 5000 :

Fig 4. Numbers  up to 5000, with primes in red.

Our 44 spirals, 20 of which holds primes, are still here.
Why just 20 ? see above.
We now expect to see 333 or 710 new spirals..

Fig 5. Primes from 1 to 20,000

Still nothing...

Fig 6. Primes from 1 to 100,000

Here we are ! some alignments are emerging.

... but we have to go up to 600,000 to see them. (on th below image, do not trust "holes" in the pattern : click on the image to see it at the normal resolution)

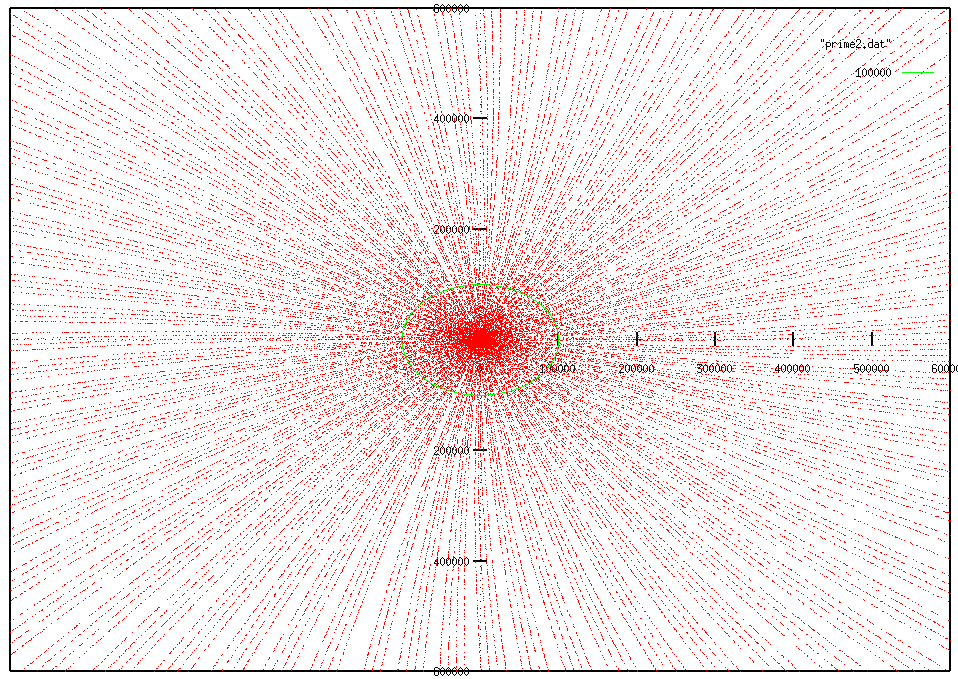
fig 7. Primes up to 600,000

We have 280 lines (below you will see these are spirals) of primes, but they bellong to a total of 710 that you would have seen if I had plotted all integers and not only primes (but unfortunately you would not be able to see anything because the screeen would be covered with too many points).

Let's go a little further, up to 3 millions :

Fig 8. Primes up to 3 millions

Nice figure, isn't it ? On each spiral number have the form n0 + 710k 
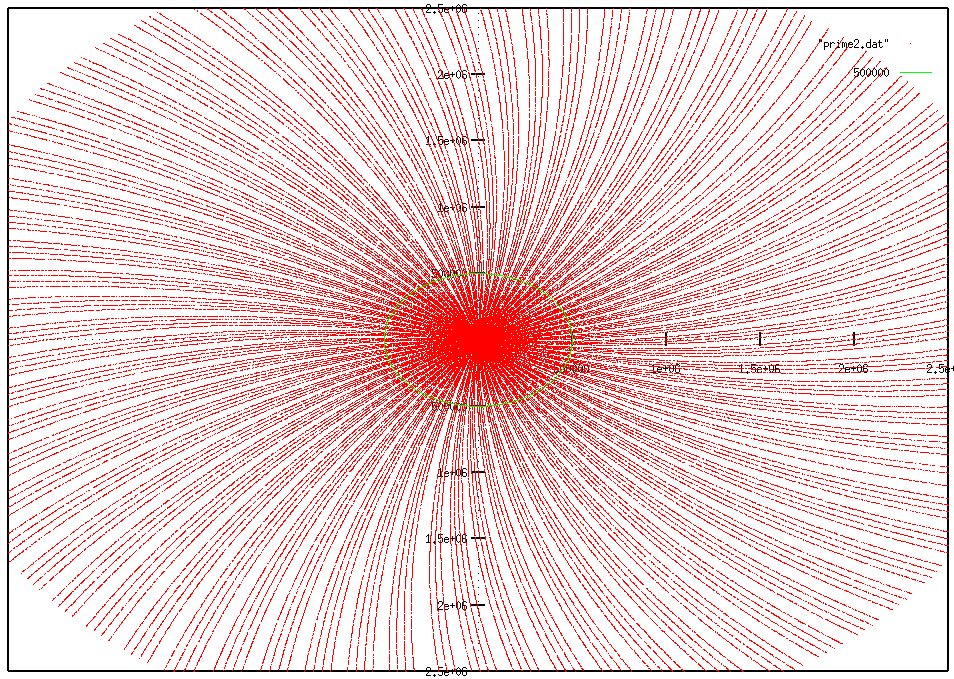
I cannot resist to give you a plot of the primes numbers up to 100,000,000. To avoid filling the image with points, I plotted only 3% of them, choosen at random (I used a special random generator designed to avoid bias, wich restes its seed at random time, depending on the current cpu time and load). The red part of the image is the previous one (primes less than 3 million)
It took two days to perform the computation of this image with a DEC alphastation 500 Mhz 64 bits Unix workstation in 1996...

Fig 9. primes up to 100,000,000 (click on image to view an enlarged version)

You see that the expected 103993 new spirals are still invisible... I can understand that !

The theory

The fact, why integers (and primes among them), are so well distributed on spirals, is well explained by the theory of continued fractions.

What is interesting is the way the distributions of prime numbers creates new spirals.

Look at fig 2 again : the very essence of that is there : holes in the distribution of primes in spirals are needed to accomodate for existence of "higher levels" spirals.

More precisely, we know from the continued fraction of 2pi that we will have six, then 19, 25, and 44 spirals of integers. Some of these cannot be "occupied" by primes (see above).  Namely the spirals that hold number 6k, 2+6k, 3+6k, 4 + 6k. This explains why primes are found only on two spirals on that six possible : 1+6k and 5+6k

But at next stage we know we will have 19 spirals : primes could be on any of them, because 19 is prime, so this is not of great value.
So we look at next stage : 25 spirals : here primes can be found on any but 0+25m and 5+25m. This means that , for instance taking the spiral 1+6k, we will have a "hole" for every number n such as n = 1+6k = 25m or 5+25m. This can never hold, because 6 and 25 are primes together.

So go at next stage : 44  spirals. Here only 20 can be "occupied" by primes :  44k+p, where p is one of 1,3,5,7,9  ,13,15,17,19,21,23,25,27,29,31, 35,37,39,41,43 (these numbers are relative primes with 44)

Update (2019) : Here is a wonderful video on prime spirals.

Others beautyfull number images : the chryzodes web page

Renaud Lifchitz page about prime spirals

> La suite : Conjectures
> index maths

This page was created in 2004