Auteur: Serge Boisse
Date: Le 28/03/2023 à 18:03
Type: web/MOC
Tags: psychologie,ia,perception,cognition
pub: oui
commentaires: ouiCopier

Principes fondamentaux de la perception

Malgré sa longueur, ce texte est extraordinairement intéressant pour quiconque s'intéresse à la philosophie, à la psychologie humaine, ou à l'intelligence artificielle (ou les trois !).
J'ai arbitrairement remplacé "cognition" par "perception" dans le titre, car Foundalis, en écrivant ce texte, avait en vue sa thèse de doctorat pour son programme Phaeaco,  qui traite essentiellement de la perception. Et parmi les cinq niveaux de la cognition, si phaeaco possède bien des éléments du niveau "modalités sensorielles" et (partiellement) du niveau "concepts", en revanche les niveaux "pensées",  "délibération" et "conscience" sont absents de phaeaco...
Serge Boisse

Un  titre alternatif pour cette page, que j'ai considéré un certain temps, a été «Lois fondamentales de la cognition".  En théorie on pourrait appeler «lois» la liste que vous pourrez voir ci-dessous, dans le sens où chaque agent cognitif suffisamment complexe les suis nécessairement : il est au-delà de la volonté humaine ou de la conscience d'essayer de les éviter. Mais j'ai opté pour le terme «principes» afin de souligner que si quelqu'un prétend avoir construit (programmé) un agent cognitif, alors l'agent doit apporter la preuve qu'il respecte les principes énumérés ci-dessous. Je soutiens que moins un agent emploie ces principes,  moins l'agent est cognitivement intéressant.

Contenu: 

Principe 1:  Principe 1 : Identification de l'objet (catégorisation)
Principe 2 Principe 2 : Analyse minimale («rasoir d'Occam»)
Principe 3 Principe 3 : Prédiction des objets (compléter les motifs)
Principe 4 Principe 4 : Distillation de l'essence (Créer des Analogies)
Principe 5 Principe 5 : Estimation des quantité et de comparaison (Perception de la numérosité)
Principe 6 Principe 6: Construction des Association par les co-occurrence (apprentissage Hebbien)
Principe 6½ Principe 6 ½: Affaiblissement temporel de la rareté (apprentissage par l'oubli)
Principe 7 Principe 7 : Codage et Décodage (CODEC perceptuel)

Principe 1 : Identification de l'objet (catégorisation)

Dans son influent essai "Six EasyPieces ", Richard Feynman introduit la description de «la mère de toutes les expériences de physique" à savoir la célèbre expérience de deux fentes d'Young, (1) parce que les résultats de nombreuses autres expériences en physique quantique peuvent être ramenés aux observations effectuées dans l'expérience des deux fentes. De manière analogue, y a-t-il dans les sciences cognitives des exemples qui peuvent servir de «Pères de tous les problèmes cognitifs» ? La réponse est oui ! Considérez la figure 1.1 :

fig 1.1 Le problème fondamental de la perception : que voyez vous sur cette figure ?

La question de la figure 1.1 est: «Qu'est-ce qui est représenté?" La plupart des gens répondraient: ". Deux groupes de points" (2) (3) Il est bien sûr possible de répondre: «Juste un tas de points", mais ce serait une réponse incomplète, celle d'un mec TRÈS paresseux. Qu'est-ce qui fait que les gens classent naturellement les points comme appartenant à deux groupes ? C'est évidemment leurs distances mutuelles, qui, grosso modo, se divisent en deux catégories. Via l'utilisation d'un ordinateur, on peut facilement écrire un programme qui, après avoir attribué des coordonnées x et y pour chaque point, atteindra la même conclusion à savoir, qu'il y a deux groupes de points dans la figure 1.1. (4)

Pourquoi ce problème est-il fondamental? Eh bien, jetons un oeil à notre entourage : si vous  êtes dans une pièce, vous pouvez voir les murs, planchers, plafonds, des meubles, le présent document, etc. Vous pouvez également envisager un cadre plus naturel, comme dans la figure 1.2, où deux perroquets sont présentés perchés sur une branche. Notez, cependant, que la rétine de nos yeux envoie seulement des  "pixels"individuels , ou des points, au cortex visuel, à l'arrière de notre cerveau (voir une approximation de ceci figure 1.3). Comment arrivons-nous à voir des objets dans une scène? Pourquoi ne voyons nous pas les points individuels?

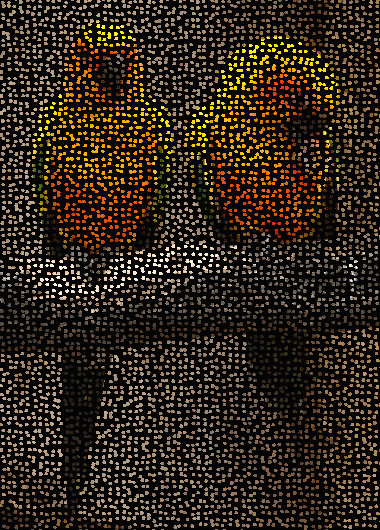
fig 1.2 Image de deux perroquets "Conure soleil" (Aratinga solstitialis) perchés sur une branche

fig 1.3 Conversion de l'image précédente en pixels comme le fait la rétine (il faut supposer que chaque pixel a une seule couleur)

La Figure 1.3 représente ce qui sort de la rétine : chaque point est issu d'un bâtonnet ou d'un cône (en général un cône) de la rétine de l'œil, et a une «couleur» uniforme (teinte, luminosité et saturation) (5). Puis Le cerveau "fait quelque chose" avec les points, et en conséquence nous voyons les objets. Ce que le cerveau fait (entre autres), est qu'il regroupe les points qui «vont ensemble». Par exemple, la plupart des points qui viennent de la poitrine des oiseaux de la figure 1.3 sont de couleur jaunâtre, de sorte qu'ils forment un groupe (une région) ; Les points  du ventre des oiseaux sont plus orangé, de nouveau, ils «vont ensemble», formant une autre région. Les points jaunes et orange de ces deux régions  sont très différents des points du fond gris-brun, de sorte que ces derniers forment une autre région (ou plusieurs). Le nombre de régions qui seront ainsi formées dépend d'un paramétrage qui détermine quand les points sont "assez proche" ( à la fois physiquement et en couleur ) afin qu'ils soient regroupés dans le même groupe. En réalité, la reconnaissance visuelle d'objets est beaucoup plus complexe : le cortex visuel comprend des détecteurs de bord, des détecteurs de mouvement, des neurones qui répondent à des pentes et des longueurs, et une foule d' autres machines visuelles spécifiques qui ont été perfectionnées par l'évolution ( par exemple, voir Thompson, 1993). Mais une première étape utile vers l'identification des objets peut être réalisée en résolvant le problème de regroupement de points. Notez que par la résolution du problème d'identification des objets nous ne percevons pas immédiatement " deux oiseaux " dans la figure 1.2 ( ce serait la reconnaissance d'objets ) , mais simplement que " il y a quelque chose ici, quelque chose d'autre là,..." et ainsi de suite. La reconnaissance est l'étape suivante.

Regardez à nouveau à la figure 1.1 : dans cette figure, les points vont de pair et forment deux groupes, tout simplement parce qu'ils sont physiquement proches les uns des autres, c'est à dire que leur "proximité " a une caractéristique unique : la proximité physique, à deux dimensions, x et y. Mais dans la figure 1.3, les points sont appariés non seulement en raison de la proximité physique, mais aussi à cause de la couleur : ainsi, dans la figure 1.3 la "proximité" des points dépend de plusieurs caractéristiques (elle possède des dimensions supplémentaires ). Si la couleur elle-même est analysé en trois dimensions ( teinte, saturation et  luminosité ) , nous avons un total de cinq dimensions pour la proximité des points dans la figure 1.3. De plus, dans le monde réel  le traitement de la vision prend en compte une troisième dimension de proximité physique ( à savoir la profondeur, résultant de la comparaison de la disparité des petits points entre les deux images légèrement différentes formées par chaque oeil ), et il peut aussi prendre en compte le mouvement comme une caractéristique supplémentaire qui peut avoir priorité sur les autres ("les points qui se déplacent ensemble appartiennent à un même objet" ). Ainsi, le concept de " proximité de points », simple en apparence, est en réalité un concept multidimensionnel, même pour la simple tâche de l'identification des objets vus.

Considérons maintenant un problème apparemment différent ( mais qui se révélera être le même en substance ) : dans notre vie de tous les jours nous percevons des visages appartenant à des personnes provenant de différentes parties du monde. Certains sont originaires d'Asie de l'Est, d'autres des pays africains, d'Europe du Nord, et ainsi de suite. Nous ne voyons pas ces visages tous à la fois, mais au cours des décennies de notre vie. Nous continuons à les voir dans nos rencontres personnelles , dans les magazines, programmes TV, films, écrans d'ordinateur, etc Pendant toutes ces années nous pourrions former des groupes de visages, et même des groupes au sein des groupes. Par exemple, dans le le groupe « européen » pour le visage, on peut apprendre à discerner quelques visages typiquement allemands, français, italiens, et ainsi de suite, en fonction de notre expérience. Chaque groupe a un élément central, un «prototype », le visage le plus typique qui à notre avis, lui appartient, et nous pouvons dire à quel point un visage donné est éloigné du prototype du groupe. ( Notez que le prototype n'a pas besoin de correspondre à un visage existant, c'est juste une moyenne. ) Ce problème n'est pas très différent de celui des figures 1.1 et 1.3 : chaque point correspond à un visage, et il y a un grand nombre de dimensions, prenant en compte chacune une caractéristique mesurable du visage : couleur de la peau, distances entre les yeux, ou entre les yeux et les lèvres, la longueur des lèvres, de la forme du nez, et un très grand nombre d'autres.

Ainsi, "l' espace des visages" a un grand nombre de dimensions. Nous pouvons imaginer un point central pour chacun des deux groupes dans la figure 1.1, situé au barycentre ( le centre de gravité ) du groupe, analogue au visage prototype d'un groupe de personnes. ( Et, encore une fois, le point au barycentre est imaginaire, il ne correspond pas à un véritable visage. ) Mais il y a des différences : contrairement à la figure 1.1, les visages sont probablement disposés dans une distribution gaussienne autour du visage prototype ( Figure 1.4 ), et nous les percevons de manière séquentielle au cours de notre vie, et non tous à la fois. Cependant, de façon abstraite, le problème est le même .

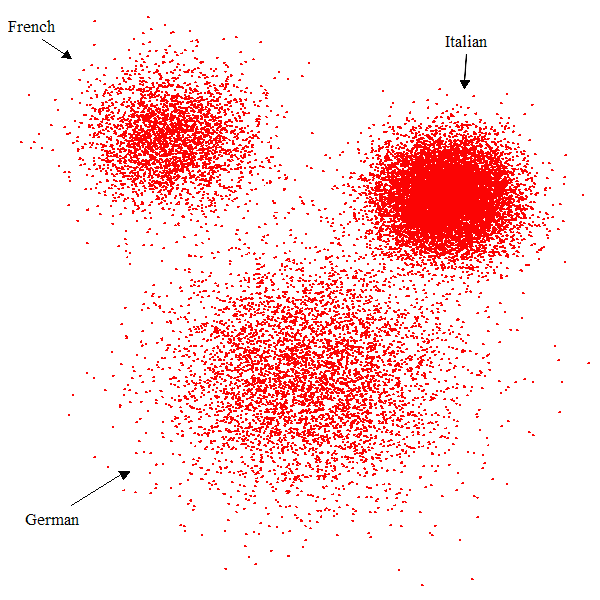
Figure 1.4 : espace abstrait des visages (en le supposant bidimensionnel)

Mais la vision n'est qu'une des modalités sensorielles de la cognition humaine. Tout comme nous résolvons le problème du groupement et de la catégorisation de visages nouveaux en les assignant à des groupes connus ou en leur permettant de se porter candidats à la création de groupes nouveaux, nous résolvons continuellement des problèmes abstraits de "formation de groupements, tels que la catégorisation des caractères des gens. Nous apprenons ce qu'est un caractère arrogant typique, un naïf typique, et ainsi de suite. Les dimensions dans ce cas sont des traits de personnalité abstraite, comme la cupidité, l'altruisme, la crédulité- scepticisme, etc. De même, dans la modalité sensorielle de l'audition, nous classons les airs de musique : classique, jazz, rock, country, etc.

Dans chacun de ces exemples ( les points de la figure 1.1, les pixels des objets, les visages des gens, des caractères des gens, etc ), nous ne sommes pas conscients des dimensions impliquées, mais les machines cognitives de notre subconscient parviennent à les percevoir et à les traiter. La machinerie cognitive qui traite les dimensions percéptuelles n'est pas précisément connue à ce jour, mais le résultat observé de ces traitements a été résumé dans un ensemble de formules lapidaire, connu comme le Modèle Généralisé des Contextes ( GCM ) ("Nosofsky 1984 ; Kruschke", 1992 ; Nosofsky", 1992 ; Nosofsky et Palmeri, 1997 ). Le GCM ne veut pas dire que le cerveau en calcule les équations ( celles de la figure 1.5), pas plus que les lois de Kepler n'impliquent que les planètes doivent résoudre des équations différentielles pour tourner autour du Soleil, et trouver certaines sections coniques ( par exemple, ellipses ) comme solutions. Au lieu de cela, comme les lois de Kepler, les formules de la GCM  figure 1.5 doivent être considérée comme une propriété émergente, un épiphénomène de certains mécanisme s plus profonds , dont la nature est inconnue à l'heure actuelle .

Équation 1

Équation 2

Équation 3

Fig 1.5 : le modèle généralisé des contextes (GCM)

La formule de l'équation 1 donne la distance dij entre deux " points ", ou " exemplaires " , dont chacun a n dimensions, et est donc un point dans un espace à n dimensions, ou un n-tuple ( x1, x2 ,..., xn ). Par exemple, chaque point de la figure 1.1 est un point dans l'espace en 2 dimensions. Les wk sont appelés les poids des dimensions, car elles déterminent l'importance de la dimension k dans le calcul de la distance. Par exemple, si quelques-uns des points dans les figures 1.1 ou 1.3 se déplacent à l'unisson, nous aimerions donner une très grande valeur pour le wk de la k-ième dimension  "mouvement avec une vitesse donnée vers une certaine direction " (ce qui en fait comprendrait non pas une mais plusieurs dimensions ) ; Simplement parce que le mouvement commun de certains points signifierait qu'ils appartiennent à un même objet en mouvement, et toutes les autres dimensions ( par exemple, la proximité physique ) seraient beaucoup moins importantes. En principe, la somme de tous les wk doit être égale à 1. Enfin, le r est souvent considéré comme étant égal à 2, ce qui transforme l'équation 1 en une " distance euclidienne pondérée " .

L'équation 2 donne la similitude sij entre deux points ( ou « exemplaires » ) i et j. Si la distance dij est très grande cette formule force leur similitude à presque 0, alors que si la différence est exactement 0, la similitude est exactement 1. Le c de la formule est une constante, dont l'effet est que, si sa valeur est grande, l'attention est accordée aux seules très grande similarités, et donc de nombreux groupes ( catégories ) seront formés, alors que si sa valeur est faible, l' effet est inverse : moins de groupes ( catégories ) seront formés. (Comment les groupes sont formés est le problème de l'équation 3, voir ci-dessous. ) On peut noter que dans certaines versions de la GCM, la quantité c ·  dij est élevée à une puissance q, de sorte que si q = 1 ( comme dans l'équation 2 ) que nous avons une fonction de décroissance exponentielle, alors que si q = 2, nous avons une décroissance gaussienne .

Enfin, l'équation 3 donne la probabilité P (G | i) que le point i sera placé dans le groupe G. Le symbole K représente " un groupe ", de sorte que la première sommation dans la formule de double- sommation du dénominateur signifie " sommer pour chaque groupe ". Ainsi, supposons que certains groupes ont déjà été formés, comme dans la figure 1.4, et un nouveau point (exemplaire ) arrive en entrée ( un nouveau visage européen est observé, dans le contexte de l' exemple de la figure 1.4 ). Comment pouvons- nous décider dans quel groupe il faut le placer ? Réponse : on calcule la probabilité P (G | i) pour i = 1, 2 et 3 ( parce que nous avons 3 groupes ) à partir de cette équation, et on le place dans le groupe ayant plus forte probabilité. Un cas particulier apparaît dans le cas où la probabilité la plus élevée se révèle être encore trop faible - inférieure à un seuil donné. Dans ce cas, nous pouvons créer un nouveau groupe. Dans la pratique, l'équation 3 est très coûteuse en temps de calcul, de sorte que certaines autres méthodes heuristiques doivent être adoptés lorsque la GCM est mise en œuvre dans un ordinateur .

Une question découlant de l'équation 3 est de savoir comment on détermine les groupements initiaux, lorsqu'il n'y a pas encore de groupes constitués, et donc que K est égal à zéro. Une réponse possible est que nous disposons également de mécanismes de regroupement différents, permettant le renforcement de certains groupes lorsque de nouvelles données arrivent, et la disparition progressive d'autres autres groupes dans lesquels aucune  ( ou peu ) de données sont affectés, jusqu'à ce que se forme une image assez claire des vrais groupes qui se dégagent à partir des données ("Foundalis et Martínez, 2007 ) . (Note de Serge Boisse : ce problème est néanmoins un problème fondamental : avant de savoir classer des objets, il faut d'abord se rendre compte qu'il y a des objets à percevoir. C'est loin d'être trivial. A mon sens, Eliszer Yudkowsky a mieux compris cela que Foundalis)

Ce qui est formidable avec les équations GCM, c'est qu'elles n'ont pas été imaginé arbitrairement par quelques informaticiens avisés, mais qu'elles ont été obtenues expérimentalement par des psychologues qui ont testé des sujets humains, et mesuré dans des conditions contrôlées en laboratoire les façons dont les gens forment des catégories. Les observations expérimentales apportent un soutien fort à l'exactitude de la GCM, selon Murphy (2002 ) .

Ce que les formules ci-dessus ne nous disent pas, c'est comment décider ce qui peut constituer une dimension d'un "point ". Par exemple : vous voyez un visage, comment savez-vous que la distance entre les yeux est une dimension, tandis que la distance entre la pointe du nez et de la pointe d'un sourcil est pas? Certes nous, les gens, nous n'avons pas à résoudre ce problème, parce que nos machines inconscientes cognitives le résolvent automatiquement pour nous, d'une manière encore inconnue ; mais lorsque nous voulons résoudre le problème de la "catégorisation de toute entrée arbitraire" par  ordinateur, nous sommes confrontés à la question de ce que sont les dimensions. Il y a une méthode, connue sous le nom "d'analyse multidimensionnelle ", qui permet la détermination des dimensions, sous certaines conditions. (6 ) Mais d'autres recherches sont actuellement nécessaires sur ce problème et des réponses définitives n'ont pas encore posée .

Les opinions diffèrent sur la théorie qui est le mieux adapté pour décrire la GCM. La question est : si des catégories sont formées et ressemblent à celles de la figure 1.4, alors comment sont-elles représentées dans l'esprit humain ? C'est la source de la célèbre dispute entre "prototype " et "exemplaire " ( voir Murphy, 2002, pour une introduction). La théorie des prototypes dit que les catégories sont représentées par une valeur moyenne ( voir Foundalis 2006, pour une approche statistique plus sophistiquée ). La théorie des exemplaires dit que les catégories sont représentées par le stockage de leurs exemples individuels. De nombreux tests de la GCM en laboratoire avec des sujets humains semblent soutenir la théorie exemplaire, même si aucun consensus n'a encore été atteint. Cependant, bien que l'architecture du cerveau semble bien adaptée pour le calcul de la GCM selon la théorie exemplaire, l' architecture des ordinateurs d'aujourd'hui est mal adapté à cette tâche. Dans Phaeaco ( Foundalis, 2006 ), une alternative est proposée, qui utilise la théorie exemplaire aussi longtemps que la catégorie reste faible en nombre d'exemples ( et donc la charge de calcul n'est pas trop lourd e), et peu à peu se décale vers la théorie du prototype lorsque la catégorie devient plus robuste et ses statistiques deviennent plus fiables. Quelle que soit la représentation interne d'une catégorie dans l' esprit humain, le résultat important est que les formules GCM semblent refléter les observations expérimentales du comportement des gens quand ils forment des catégories .

Le lecteur sans doute remarqué que cet article a commencé avec la question de l'identification d'objets, et a fini avec le problème de la formation des catégories. Comment ce changement de sujet a-t-il pu se produire ? Mais la vraie beauté du premier principe est qu'il unifie les deux notions en une seule : l'identification d'objets et la formation de la catégorie sont en fait le même problème. Il est tentant de supposer que le spectre qui commence par l'identification d'objets et se termine avec la formation de catégories abstraites a une base évolutive, selon laquelle les animaux cognitivement plus simples n'ont atteint que le " bas " de ce spectre ( l'identification concrète d'objets ), puis que lors leur évolution en des créatures plus complexes cognitivement, ils ont pu résoudre des problèmes de catégorisation plus abstraits .

La puissance du premier principe est qu'il permet à la cognition se produire d'une manière tout à fait essentiel le : sans l'identification d'objets, nous serions incapables de percevoir quoi que ce soit. Notre édifice cognitif tout entier est basé sur la prémisse qu'il y a des objets ici-bas ( les noms dans les langues ), que nous pouvons compter : un objet, deux objets ... Sur la base de l'existence des objets, on note leurs propriétés ( un objet rouge, un objet en mouvement, ...), leurs relations ( deux objets en collision, un objet sous un autre, ...), les propriétés de leurs relations (un objet en mouvement lent, un objet ennuyeusement uniforme, ...), et ainsi de suite. Soustrayez les objets de l' image, et il ne reste rien : la cognition disparaît entièrement .

Une question connexe intéressante est de savoir si il y a vraiment des objets dans le monde, ou bien si notre connaissance les concocterait simplement, comme certains philosophes l'ont affirmé ( par exemple, Smith, 1996 ). Mais je pense que ce point de vue met la charrue avant les bœufs : c'est parce que le monde est structuré dans certains schémas particuliers ( formant des agglomérations  d'unités analogues) qu'il peut s'offrir la cognition, c'est à dire  l'évolution de créatures qui ont profité du fait que les objets existent, et utilisé cette propriété pour augmenter leurs chances de survie. La cognition reflète la structure et les propriétés du monde. Le point de vue philosophique « constructivisme strict» qui nie l' existence des objets en dehors de l'esprit d'un observateur, ne peut pas expliquer l' origine de la cognition .

Note de Serge Boisse : sans être "constructiviste strict", je pense que c'est Foundalis qui met la charrue avant les boeufs : Nos sens en effet ne servent pas uniquement à décoder les perceptions, mais ils sont également capables de coder, de créer des pseudo perceptions, telles que celles que nous percevons en rêve, ou simplement en fermant les yeux.  Si le cerveau peut imaginer des choses, il peut imaginer ce que nous appelons "réalité". Plus sur ce point au principe 7.

Principe 2 : Analyse minimale («rasoir d'Occam»)

Un méta- principe très connu de la philosophie, connu sous le nom « rasoir d'Occam » ( souvent orthographié à tort " Ockham" ), affirme que la plus simple de deux ou plusieurs théories concurrentes et égales par ailleurs est préférable. Habituellement, toutefois, aucune justification n'est donnée pour le rasoir d'Occam : il est simplement supposé que c'est une règle utile pour la sélection des ensembles de principes philosophiques ( d'où, le «méta- principe » ). Mais la justification existe, et elle est profondément enracinée dans la façon dont notre connaissance fonctionne. Sans le savoir, nous utilisons le rasoir d'Occam à chaque instant, tout au long de notre vie. Prenons l'exemple suivant :

"figure 2.1 En quoi consiste cet objet ? De quoi est-il fait ?
"

"
Que représente la figure 2.1 ? Comment décririez-vous ce que vous voyez ? On peut dire que c'est la lettre "X" dans une certaine police de caractère simple, ou le symbole de la multiplication. OK, mais supposons que vous ne connaissez pas ces symboles, que vous ne savez rien alphabets occidentaux ou de la notation mathématique, et je vous repose la même question. Vous pourrez encore décrire d'une manière ou d'une autre ce que vous voyez. Vous pourriez dire qu'il il s'agit de deux bâtons inclinés, placé au-dessus de l'autre. En d'autres termes, vous verriez l' objet ci-dessus comme ceci:"

Fig 2.2. La décomposition "normale" de l'objet X.

C'est la façon "normale" que pratiquement toute personne utiliserait pour décrire l' objet. ( Une expérience avec un certain nombre de personnes aiderait à éliminer tout doute. ) Il en existe d'autres. Voici quelques-uns des moyens «anormaux» ( inattendus )  que certaines personnes pourraient choisir pour le décrire :

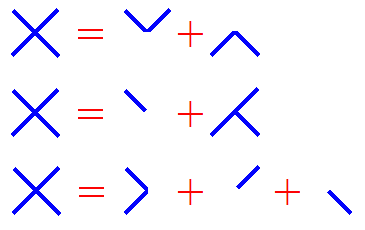
fig 2.3 : Quelques décompositions "anormales" de l'objet X

J'appelle ces moyens «anormaux » parce que très peu de gens choisissent l'un d'eux pour rendre compte de comment ils voient l' objet. ( Si certains le font, personnellement, je crois qu'ils ont essayé de démontrer leur créativité - d'une manière assez peu convaincante - au lieu de rapporter ce que la plupart des gens voient normalement )

Pourquoi la plupart des gens l'utilisent-t-ils la description X = \ + / ? Parce que le " \ + / " constitue une description minimale par rapport à toute autre manière de décomposer l'objet X. Si vous voulez voir pourquoi cette description est minimale ( la plus courte ), essayez de dire tout haut de quoi X est constitué de selon elle :

X est constitué de deux segments de droite de longueur égale, le premier est incliné de 45 °, et le second de -45 °. Leurs milieux coïncident .

C'est tout. Si cela n'est pas assez court pour vous, essayez de décrire à haute voix la première des descriptions «anormales » de l' objet, soit X =  " V + Λ " :

X est constitué de deux morceaux : le premier est constitué de deux segments de droites d'égale longueur, inclinés de 45 ° et -45 °, et qui se rencontrent à leur  point le plus bas", que nous appellerons un sommet, le second morceau est symétrique du premier par rapport à l' axe horizontal, et les deux morceaux se rencontrent à leurs sommets .

C'est plus long, non? N'essayez même pas d'écrire le deuxième ou le troisième exemple «anormal » : les descriptions seront forcément encore plus longues.

Ce que nous faisons lorsque nous trouvons inconsciemment la description minimale de la structure d'un objet, c'est que nous appliquons automatiquement le rasoir d'Occam : on élimine toute "théorie" superflue, trop longue, sur comment l'objet est fait, et nous nous en tenons à la plus courte. Nous faisons cela sans que personne ne nous ait dit explicitement comment le faire, ou pourquoi le faire. C'est simplement le fonctionnement de notre appareil visuel. S'il n'en était pas ainsi, nous aurions une image très confuse et très complexe du monde, plutôt que la compréhension de la structure des objets .

Des descriptions minimales ne sont pas préférable uniquement dans le cas des dessins artificiels, tels que le X de la figure 2.1. Considérez ce qui suit :

Fig 2.4 Quelle est la manière normale de décrire cette image ?

Combien de guépards y-a-t-il dans la figure 2.4 ?  Une réponse inattendue ( «créative» ?) pourrait être qu'il y a trois, ou peut-être deux guépards vivants : on verrait la tête et les pattes avant de l'un, l'arrière des jambes et la queue d'un autre, et un morceau de la peau d'un troisième qui serait suspendue comme une draperie derrière les troncs d'arbres. Pourquoi n'est- ce pas ce que nous voyons spontanément ? Pourquoi nous ne voyons jamais ces décompositions stupide du monde ? Parce que dans certaines situations, c'est une question de vie ou de mort que de comprendre correctement ce que nous voyons , de formuler la théorie la plus simple (" Un guépard ! " ) et de prendre une action appropriée (" attrapez cette lance ! " ) .  Ceux de nos ancêtres qui ne pouvaient pas appliquer le rasoir d'Occam ne vivaient pas assez longtemps pour propager leurs gènes - et pas seulement à cause des prédateurs, bien sûr, mais en général, en raison de leur incapacité à analyser correctement le monde. Notez que le terme «ancêtres », ci-dessus, ne se réfère pas seulement à nos ancêtres humains .

La capacité d' analyser l'environnement d'une manière utile et de former la «théorie» la plus simple en ce qui concerne sa structure est une capacité enracinée dans des temps beaucoup plus anciens que les origines de l'homme. Non équipé d'une version du rasoir d'Occam, un animal à la cognition rudimentaire pourrait constituer un tas de " théories "inutiles" , telles que supposer qu'il y a un prédateur qui se cache derrière chaque rocher et dans chaque crevasse. Un prédateur pourrait également formuler une «théorie» tout aussi inutile  sur les aliments ; ainsi en inspectant un rocher ou une crevasse, et en ne trouvant pas de nourriture, l' animal pourrait en conclure que la nourriture a disparu juste un moment avant l' inspection (7 ) Un tel comportement forcerait les animaux. à gaspiller des ressources précieuses, et serait certainement une " mauvaise idée " si la survie dans le monde naturel est en jeu. Ainsi, très probablement, le rasoir d'Occam est aussi ancien que la cognition animale elle-même .

Il est intéressant de noter dans le même contexte une illusion visuelle célèbre qui apparaît souvent dans les manuels de psychologie, l' illusion de Kanizsa :

Fig 2.5 L' illusion du triangle de Kanizsa, une autre application du second principe

Dans la figure 2.5, un triangle équilatéral blanc semble exister au cœur même de la figure, reposant sur son sa base, et se superposer (par occlusion ) sur un autre triangle équilatéral tracé pointe vers le bas, ainsi que sur trois cercles noirs autour de ses sommets. C'est la fameuse "illusion du  triangle de Kanizsa ". En réalité, il n'y a pas de triangle blanc au centre, et il n'existe aucun triangles ou cercles. Tout ce qu'il y a, c'est trois figures noires qui ressemblent à " pacman " , faisant face à trois directions différentes, et des morceaux de lignes droites formant trois angles. Mais si vous essayez de donner une description précise en langage naturel de ce que je viens de dire, vous verrez qu'elle est beaucoup plus longue que celle que j'ai déjà donné au début de ce paragraphe («un triangle blanc équilatéral ...") - essayez en décrivant la direction vers laquelle chaque angle pointe, si vous n'êtes pas convaincus. Donc, nous ne voyons pas pacman et les lignes droites, mais des triangles et des cercles .

Les exemples ci-dessus proviennent de la modalité sensorielle de la vision. Mais, comme il est bien connu dans les sciences cognitives, la vision est à la base de notre raisonnement abstrait. Les exemples de situations où nous employons le langage de la géométrie pour parler abstraitement sont treize à la douzaine : " elle a intérêt à filer tout droit", " au point où on en est", " ce film a un ennuyeux, scénario, très plat", " c'est un sujet difficile avec une courbe d'apprentissage lente", "s'il vous plaît évitez les circon_locutions , utilisez une langue plus _directe", "une relation triangulaire entre les gens","soyez honnête, et elle vous donnera des réponses carrées", "nous ne pouvons pas tout inclure dans le discours, nous devons en couper certains coins", et ainsi de suite. George Lakoff, parmi d'autres linguistes, ont très clairement indiqué que la pensée abstraite est basé sur le langage de la géométrie, qui décrit le monde de la vision. Lakoff est appelle cela des métaphores ("Lakoff, 1980"). D'autres chercheurs en sciences cognitives, tels que Douglas Hofstadter", appellent cette capacité création d'analogie, et pensent qu'elle repose à la base de notre cognition, c'est à dire, de ce qui nous rend humain ("Hofstadter, 2001") - un point qui sera examiné plus avant dans le contexte du quatrième principe .

Par conséquent, lorsque nous formerons une théorie explicative, nous ne faisons rien d'autre que d'appliquer des notions visuelles et géométriques à un niveau plus abstrait. En géométrie, une théorie peut être aussi complexe que la démonstration d'un théorème, ou aussi simple que l' analyse d'une figure géométrique. Dans le cas d' une démonstration d'un théorème, les mathématiciens cherchent consciemment la plus courte, une preuve plus simple, parce que c'est ce qui plaît le mieux à leur intuition ( généralement sans être en mesure d'expliquer pourquoi leur sens mathématique les amène à avoir cette préférence ), tandis que dans le cas de l'analyse d'une image, tout le monde préfère la description minimale, et ce inconsciemment, parce que c'est la façon dont nous avons évolué pour fonctionner, pour les raisons expliquées précédemment. De même, dans la science, une théorie scientifique est préférable quand elle est plus concise que l'autre et n'a pas de complications inutiles tout en expliquant le même corpus de données ( cf. l' adoption de la théorie héliocentrique, qui a remplacé celle inutilement complexe du géocentrisme ). Mais le principe fondamental est le même dans tous les cas : appliquer le rasoir d'Occam pour trouver ( consciemment ou inconsciemment ) la plus simple analyse, la preuve la plus courte, la plus vigoureuse théorie. Guillaume d' Occam a pu exprimer son célèbre «rasoir » dans les 13e et 14e siècles, mais ce principe fait partie de la cognition humaine - et probablement même de la cognition animale - depuis des temps immémoriaux. Sans lui nous ne pourrions pas comprendre la structure du monde .

Enfin, il faut préciser ce qu'on entend par "minimal " dans le terme " description minimale ". Certains lecteurs pourraient interpréter cela comme voulant dire minimal au sens mathématique, c'est à dire une description absolument plus courte que toute autre, et argumenter qu'une telle description ne peut pas toujours être trouvée. En effet, il a été prouvé qu'il n'est pas en général possible de découvrir la description absolument minimale d'un élément d'information : le problème est non calculable. Mais la précision mathématique est généralement loin d' être une caractéristique de la cognition, qui est fluide et souple. Ainsi, par le terme «minimal », on entend dans un sens approximatif, " assez bon pour faire le travail ", et l'analyse heuristique peut toujours être utilisée pour trouver des solutions assez bonne. Dans le logiciel Phaeaco, la méthode utilisée pour parvenir à des descriptions minimales pour des objets tels que le X de la figure 2.1 est que les morceaux de lignes droites ( qui sont considérées comme primitives ) sont suivis (analysés) dans leur extension maximale : ainsi, un «X» sera considéré comme constitué d'un / et un \ .

De même, un A sera analysé comme / plus \ plus -, plutôt que comme un triangle isocèle avec deux " jambes " obliques . Fait intéressant, ces décompositions sont les moyens habituels par  lesquels les gens tracent des lettres telles que X et A sur le papier avec un stylo. Au-delà des primitives simples, les objets sont considérés comme étant constitué d'éléments connus ( extraits de la mémoire à long terme ). Les informations non visuelles (ce qui est hors de la    portée actuelle de Phaeaco ) peuvent sans doute s'appuyer sur les principes visuels et  les adopter tous sur le chemin de la pensée abstraite .

Principe 3 : Prédiction des objets (compléter les motifs)

Considérez la figure suivante :

Fig. 3.1 Que voyez vous ici ?

Beaucoup de lecteurs sont sans doute en mesure de dire non seulement que la figure 3.1 montre " un visage ", mais aussi personne en particulier qui est représentée. Pourtant, l'image ne montre même pas un visage, mais seulement différentes parties de celui-ci : un œil, un nez, une partie du front, des cheveux. C'est plus que suffisant, cependant, pour que tout le monde se rappelle le concept de « visage » et, pour certains ( beaucoup, peut-être ) pour rappeler le concept plus spécifique " Albert Einstein ". Ce qui se passe est que nous nous rappelons le tout sur la base de certaines parties de celui-ci. Maintenant, considérons ce qui suit :

2, 4, 6, 8, 10, 12, 14, ...

Fig 3.2  Quel est le nombre qui suit ?

Cela ne prend pas plus de quelques secondes pour réaliser que la suite de la figure 3.2 est le début de celle des nombres pairs positifs, et ainsi de prédire que le prochain numéro de cette suite devrait être 16. Le terme approprié dans ce contexte est " raisonnement inductif ", c'est à dire, qu'à partir de quelques exemples nous les utilisons inductivement pour comprendre la règle de base (" nombres pairs ", dans la figure 3.2 ), et par extrapolation, nous prédire les futures instances .

Les figures 3.1 et 3.2 montrent des exemples de " complétion de motif ", une capacité cognitive très important e. La différence entre les deux exemples est que l' information de la figure 3.2 est séquentiel le, alors que celle de la figure 3.1 ne l'est pas : nous pourrions nous donner à voir une partie ou des parties du visage d'Einstein et encore prédire le reste ( ou simplement atteindre le concept " visage", si l' information n'est pas suffisante pour atteindre " Einstein " ). En revanche, l' ordre est important dans le cas de la figure 3.2. Le fait que la tâche de  prédiction des objets ( ou la reconnaissance d'un motif ) est séquentielle ou non dépend de la modalité d'entrée. Les modalités visuelles et  haptiques ( tactile, du toucher ) sont en grande partie non- séquentielles : si nous tenons un objet dans les mains, nous pouvons généralement dire ce que c'est les yeux fermés, sans analyse séquentielle, alors que l'information auditive est nécessairement séquentiel le, ce qui fait que la perception du langage et de la musique est une tâche séquentielle : après avoir entendu une partie d'une phrase, on peut souvent prévoir à peu près ce que seront les mots suivants ( ce qui provoque parfois des gens à adopter la fâcheuse habitude de d'interrompre les autres, avec le sentiment qu'ils n'ont pas besoin d' attendre que l'idée soit exprimée en toutes lettres) ; De même, après avoir entendu une partie d'un morceau familier de musique, on peut généralement prédire exactement ce que sera la suite , car il n'existe pratiquement aucune variation dans la façon dont un morceau familier est joué ( s'il y en a, nous le percevons comme un couac de l'instrumentiste ) .
"
Comme dans le cas des principes précédents , la capacité à prédire et à compléter des modèles n'est pas propre à l'homme, mais tire son origine dans la cognition animale. En effet, elle est d'une importance vitale pour la survie. Considérez un animal confronté à la vue de la figure 3.3 :

Fig 3.3  Paire de mâchoires flottant sur le fleuve ?

"
L' animal pourrait peut-être vivre un peu plus longtemps s'il pouvait «prédire » que ce n'est pas seulement une paire de mâchoires flottant sur la rivière qui sont impliqués, mais un  d'hippopotame tout entier qui se trouve en dessous. Le guépard de la figure 2.4 est un autre exemple de l' utilité de former un tout correct à partir de quelques parties. La prédiction séquentielle est également à la portée des animaux, comme des expériences de psychologie animale l'ont montré .

Le principe de complétion des formes est directement à l'œuvre dans les cas où le contexte nous suggère de compléter ou d'interpréter l'information manquante ou ambiguë d'une façon ou d'une autre. Voici un dessin ambigu bien connu  :

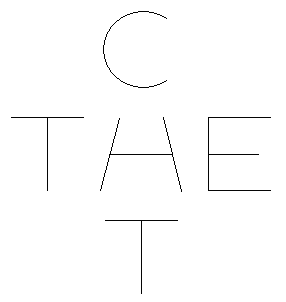
Fig 3.4. La lettre ambiguë au milieu peut être considérée comme un «A » ou un « H »

Si nous lisons horizontalement la figure 3.4, nous voyons le mot " THE ", donc nous interprétons la lettre du milieu comme un «H», mais si on lit verticalement, on voit le mot «CAT», en interprétant la lettre du milieu comme un " A ". Dans ce cas, le contexte nous aide à interpréter la forme ambiguë d'une manière ou d'une autre, donc nous fournit les éléments manquants. Dans d'autres cas, le contexte devient une aide indispensable pour compléter les informations manquantes, par exemple lorsque vous lisez un texte composé de phrases longues : vous ne voyez pas chaque lettre individuelle que vous lisez, comme en témoignent les expériences qui suivent les saccades oculaires ( mouvements rapides des yeux ) ; en réalité, vous sautez de mot en mot, passant souvent "au dessus" de petits mots sans les analyser, et vous remplissez les informations manquantes par le biais de ce que vous vous attendez à voir, c'est à dire, au moyen du contcxt e. ( Si vous avez repéré l' erreur dans le dernier mot de la phrase précédente, félicitations, si vous l'avez manqué, vous avez interprété le c comme un e, aidés par le contexte. )

Encore une fois, il y a la question d'implémentation de la prédiction des objets. Comment le cerveau y parvient-il, et comment peut-on la mettre en œuvre dans un ordinateur ? Les travaux sur les réseaux de neurones formels ont montrés qu'il est relativement facile de réaliser une forme rudimentaire de complétion de motif dans les ordinateurs, en supposant l'invariance de l'entrée, à savoir que le réseau ne doit pas échouer complètement si l' entrée est déplacée, tournée, ou zoomée dans une certaine mesure. Le cerveau, cependant, ne suppose pas l'invariance de l'entrée, mais il la réalise. La manière exacte dont il procède n'est pas connue avec précision encore, mais cette question neurobiologique ne nous intéresse pas ici. Comme la manière d'atteindre invariance d'entrée dans les réseaux neuronaux n'est pas encore connue, et parce que le matériel informatique est basé sur une architecture totalement différente par rapport à celui des neurones, d'autres approches de calcul peuvent également avoir de la valeur.

Dans Phaeaco il existe un système de traitement visuel primaire et un secondaire. Le système secondaire ( qui n'est pas nettement séparé du primaire ) est responsable de la construction des représentations internes de ce qui est vu. En fait si, tandis que la représentation est en cours de construction ( mais n'est pas encore complèt e) un concept est atteint et suffisamment activé dans la mémoire à long terme ( au moyen d'un " schéma d'indexation " qui accélère l'accès à la mémoire à long terme ), alors le traitement secondaire peut en conclure quelque chose comme : «Bon, je sais ce que je vois, je n'ai pas besoin d'une confirmation ultérieure", et effectivement arrêter le traitement primaire avant la fin de l'examen de l'entrée ( Ceci afin d' économiser des du temps de calcul ; un organisme biologique n'aurait pas nécessairement besoin de le faire ). C'est la façon dont Phaeaco « voit sans voir " tout ce qui est visible - une capacité très importante pour la prédiction des objets .

Principe 4 : Distillation de l'essence (Créer des Analogies)

Le fait d'identifier les objets, de percevoir leur structure minimale, et de les prédire à partir de leurs parties ne suffit pas à acquérir une  compétence cognitive du niveau de celle de l'homme. Quelque chose de plus est nécessaire. Cet ingrédient supplémentaire, dont on ne sait pas si certains animaux non- humain le possèdent ou pas, est la capacité à ne pas se laisser distraire par les détails superflus et de saisir le noyau essentiel d'un objet, un événement, une situation, une histoire, ou une idée. Considérons la figure suivante :

Fig 4.1  Quelle est la particularité des pixels rouge dans la figure de l'homme ?

La Figure 4.1 montre une silhouette humaine sur la gauche ; au milieu, certains pixels ont été soulignés en rouge, et représentés isolément sur la droite. Ces pixels ne sont pas aléatoires : ils ont été construits algorithmiquement par un programme, et ont la propriété que chacun est au " milieu ", c'est à dire, aussi loin que possible de la " frontière " de cette forme ( les pixels qui séparent la noirceur de la blancheur ). L'algorithme spécifique qui identifie ces pixels n'est pas important. Ce qui est important, c'est qu'il est algorithmiquement possible - une tâche facile, en fait - à la fois pour le cerveau et un ordinateur, d'arriver à quelque chose comme la forme en bâtons sur la droite. Les enfants, dès le début de leur développement, utilisent généralement des formes en bâtons pour dessiner les gens (sauf qu'ils tracent la partie la plus importante, la tête, avec un ovale ou un cercle ). En musique, l' analogue de « dessiner le bonhomme allumette " d'une mélodie consiste à fredonner ( ou siffler, ou jouer sur un piano avec un seul doigt ) les notes les plus fondamentales de celle-ci, à la bonne hauteur et avec la bonne durée .

Lorsque nous percevons le " milieu " dans la figure 4.1 sur la gauche, nous faisons abstraction des " détails sans intérêt ", tels que la manière exacte dont les pixels de la frontière forment des lignes brisées. La figure humaine pourrait comporter " cheveux " à la frontière ( pixels parasites ), ou des pixels de différentes couleurs, mais nous serions encore en mesure de percevoir le  milieu de celle-ci. Mais la capacité à identifier l '«essence » des choses ne se limite pas à des objets concrets, elle devient encore plus polyvalente - vraiment étonnante - dans des situations les plus abstraites. Prenons l'exemple suivant :

Dans son livre Fluid Concepts and Creative Analogies (Concepts fluides et Analogies Creatives), Douglas Hofstadter raconte une situation anecdotique, dans laquelle il observait sa fille Monica, qui avait juste un peu plus d'un an et qui jouait avec un Dustbuster ( un aspirateur jouet à main fonctionnant sur piles ). Monica appuyait sur le bouton marche-arrêt , s'amusant du bourdonnement émis par le jouet. À un certain moment, elle a remarqué un bouton de forme différente sur le jouet, et bien sûr elle essayé de pousser celui-là, aussi. Elle a été déçue si, parce que c'était le bouton de déverrouillage pour le couvercle qui maintenait le sac à poussière dans le jouet, et après quelques échecs de plus, elle a renoncé. Son père s'approcha et lui montra ce que le deuxième bouton faisait, mais cela n'impressionna pas beaucoup Monica .

Soudain, son père eut un flash en se souvenant de quelque chose qui s'était passé dans son enfance. Il avait appris, à  huit ans, à appliquer différentes opérations arithmétiques sur les nombres, et l'une des opérations qui lui plaisaient beaucoup était l' exponentiation. ( Je soupçonne que son propre père, Robert Hofstadter - le lauréat 1961 du prix Nobel de physique - doit avoir joué un important rôle à cet égard ! ) Un jour, le jeune Doug avait remarqué la notation mathématique figurant sur un des documents de son père sur la physique, et avait été attiré par l' utilisation omniprésente des indices. Êtant familier avec les merveilles des exposants, il sauta sur la conclusion que les indices devaient cacher un monde tout aussi merveilleux que celui des exposants en arithmétique.  Mais il fut déçu quand il demanda à son père et que celui ci lui expliqua que les indices sont simplement utilisés pour distinguer une variable d' une autre (Hofstadter, 1995a ) .

L'histoire d'Hofstadter est un exemple quintessentiel (et encore étonnant ) d'une analogie. Il y a deux situations analogues qui sont analysées, et il y a un tronc commun, une essence, qui reste invariante entre les deux situations. Dans cet exemple, l' essence comprend une relation père- enfant, un "jouet " qui comporte un seul élément avec lequel l'enfant a du plaisir à jouer, un second élément similaire sur le jouet qui est soudain découvert par l' enfant, et une déception après que l'enfant soit informé par le père que ce deuxième élément ne fait rien de très intéressant .

Cependant, quand une situation analogue vient à l'esprit, on ne pense généralement pas consciemment à l' essence de ces deux situations. Il est possible de le faire après un examen attentif, comme je l'ai fait dans le paragraphe précédent, mais, à moins que nous le recherchions explicitement, le tronc commun nous échappe presque toujours. Ce noyau, l' essence, est aussi inconscient que les pixels du milieu de la figure 4.1, que nous n'avons pas à imaginer consciemment à moins qu'on nous demande explicitement de le faire. Pourtant, le noyau doit exister, sinon nous serions incapables de dessiner des figures en bâton, ou de faire des analogies comme celle-ci .

Et ce n'est pas seulement une capacité a priori exotique, "la création d' analogie ", qui est en cause. La capacité de percevoir l'essence et de rejeter les détails non essentiels nous permet de penser à des concepts tels que «triangle » et « cercle », sans nous soucier de l' épaisseur des lignes qui composent ces objets géométriques, ou même des lignes elles-mêmes. Ainsi, nous pouvons abstraire ces concepts totalement, et parler d'une " relation triangulaire, entre des gens ", ou de " mon cercle d' amis ". La capacité à percevoir l' essence des choses a conduit l'ancien philosophe Platon à affirmer qu'il existe un monde immatériel des essences, plus profond que le monde perçu, et que, lorsque nous parlons d'un cercle ( ou d'une table, ou de quoi que ce soit), nous avons accès à cet objet idéal, alors que notre monde matériel nous fournit beaucoup d e détails superflus. Ce fut la fameuse théorie des formes de Platon, qui a influencé la pensée occidentale pendant deux millénaires et demi .

Bien qu'aujourd'hui la théorie de Platon n'ait plus l'influence qu'elle avait autrefois, elle montre que lorsque l'antique penseur  a essayé de trouver ce qui est fondamental dans un esprit, ils s'est mis le doigt sur la tête. D'autres, les penseurs d'aujourd'hui, tels que Douglas Hofstadter, affirment que la création d'analogies est au cœur de la cognition ("Hofstadter, 2001). Cette affirmation est difficile à comprendre, parce que le terme "créer des analogies" invoque généralement pour les non-initiés d'ennuyeuses énigmes logiques de la forme « A est à B comme C est à quoi ? " Mais, au-delà des énigmes logiques, nous utilisons et nous créons de nouvelles analogies (ou métaphores, selon les termes de Lakoff - voir aussi le second principe ) tout le temps, alors même que nous parlons. Si nos pensées restaient limitées à ce qui peut être immédiatement vu, si nous étions incapables de faire des abstraction par extraction des concepts de base, nous vivrions encore dans un monde très primitif .

Plus tôt, j'ai supposé que seuls les humains ont cette capacité. Toutefois, on peut présumer que, lorsque les chimpanzés utilisent un bâton pour « pêcher » les termites et les sortir d'un trou, ils ne perçoivent pas le bâton pour ce qu'il est ( un morceau cassé d'un arbre ou un arbuste ), mais comme un objet de forme allongée solide, ce qui est l' essence même d'une branche, et qui est ce qui est important pour la tâche qu'ils veulent accomplir. Toute utilisation de quelque chose comme un outil - que ce soit une pierre brute ou un couteau suisse sophistiqué - fait usage de l'objet non pour ce qu'il est ( un morceau de rock, un morceau de métal et plastique), mais comme ce en quoi son essence profonde peut aider le possesseur de l'outil  à réaliser la tâche en cours. Même l'utilisation des jouets peut être considérée comme ayant la même fonction cognitive que celle des outils, et les mammifères et les oiseaux supérieurs sont connus pour utiliser un large éventail de jouets (8)

Fig 4.2 Une jolie jeune chimpanzée (Pan troglodytes ) utilisant un bâton et une plume comme des jouets

Certains chercheurs en sciences cognitives et en intelligence artificielle ont annoncé la construction de logiciels qui, soi-disant, peuvent  « découvrir des analogies ". Par exemple, ils disent que, étant donné les idées d'un système solaire et d'un atome avec son noyau et ses électrons en orbite, leurs programmes sont capables de découvrir l'analogie entre les deux structures. De telles revendications sont en grande partie vides de sens. ( Je préfère éviter de faire des références explicites, mais voir Hofstadter, 1995b, pour un autre point de vue critique de ces approches. )  Ce qu'ils veulent dire, c'est que une fois que quelqu'un ( une personne ) a codifié explicitement la structure d'un système solaire et celle d'un atome ,  leur programme arrive à  «découvrir » l'existence d'une analogie. Mais tout le problème repose sur notre capacité à découvrir spontanément  deux structures semblables, comme dans l'exemple de Hofstadter, ci-dessus ! Hofstadter n'a pas pensé  " Faisons une analogie maintenant ! - euh, qu'est-ce qui est l'essence de la situation que nous avons ici ?", en réalité il n'a même pas  pensé à trouver cette essence, et il n'a pas délibérément non plus cherché à apparier ce noyau et quelque chose dans sa mémoire . Tout s'est passé automatiquement .

Si quelqu'un me dit, " Voici deux structures, trouvez s'il y a une analogie entre eux et expliquez moi pourquoi ", le problème est presque résolu - je vous remercie beaucoup. Le vrai problème est : Comment pouvons-nous spontanément nous concentrer sur l' essentiel et le faire correspondre à quelque chose qui corresponde à cet essentiel ? Telle est la question cruciale dans la recherche par analogie, et, à ma connaissance, personne n'a encore répondu .

En ce qui concerne mon programme "Phaeaco", je m'abstiens de faire des déclarations grandioses telles que "Phaeaco peut découvrir les analogies ". Ce que le programme fait, c'est extraire un "noyau" de la base de données visuelles, comme le montre la figure 4.1, et utiliser cette base pour se représenter la structure de l' entrée de manière interne, puis la stocker dans la mémoire à long terme. Si une entrée visuelle avec une structure de base similaire apparaît plus tard, Phaeaco va faire correspondre les deux structures et les marquera comme étant très similaires, même si elles diffèrent dans les détails ( et il le fera automatiquement, sans que personne lui demande expressément de le faire à tout moment ). Que cette capacité puisse être augmentée à l'avenir afin que Phaeaco devienne capable d' extraire le noyau d'entités plus abstraites - comme des pensées et des idées -, cela reste à voir .

Principe 5 : Estimation des quantité et de comparaison (Perception de la numérosité)

Regardez la figure suivante :

fig 5.1  Combien voyez vous de points, sans les compter ?

Tout le monde peut estimer approximativement le nombre de points de la figure 5.1, sans avoir recours au comptage. Bien que ces estimations varient, peu de gens, voire aucun, affirmeraient qu'ils voient moins de 10 points, ou plus de 50 .

La capacité qui nous permet d' arriver à une estimation de la quantité d'objets séparés ( dénombrables )  est la perception de la numérosité ( c'est à dire de la quantité de choses ), et cette capacité obéit à certaines régularités, qui sont discutés ci-dessous .

Premièrement, plus le nombre d'entités est faible , plus  notre estimation de leur nombre est précise.

"Si, par exemple, seuls trois points sont affichés devant nos yeux, même pour une fraction de seconde, notre estimation sera presque toujours exacte : trois points. Si, toutefois, 23 points sont affichés ( comme dans la figure 5.1 ), il est fort peu probable que nous allons arriver à "23 ", peu importe combien de temps on les voit ( à condition de ne pas recourir au comptage ) " ; il est probable que notre estimation variera quelque part entre 15 et 30. Mais si l'on répète l'expérience plusieurs fois, alors l'estimation moyenne convergera vers le nombre 23 ( à condition que nous ayons reçus une formation préalable pour l'estimation d'un n ombre de points, sinon - sans formation - notre estimation moyenne pourrait converger vers un nombre un peu différent ). Dernière observation, mais non la moindre, si 100 points sont affichés , nos estimations vont varier dans un intervalle plus large : par exemple entre 50 et 150 ( par exemple - je ne fais qu'estimer  approximativement cet 'intervalle ) .

Comment pouvons nous être sûrs que l'idée ci-dessus est vrai e ? Les expériences qui permettent de vérifier cette idée n'ont pas été faites sur des personnes, mais sur des rats  "! Oui, des animaux cognitivement aussi simples que les rats sont en mesure d' estimer les le nombre des objets. Dans une expérience réalisée par Mechner en 1958, et répété par Platt et Johnson en 1971, des rats affamés étaient tenus d'appuyer sur un levier un certain nombre de fois avant d'appuyer une fois sur un deuxième levier, ce qui ouvrirait la porte d'un compartiment contenant de la nourriture (Mechner, 1958 ; Platt et Johnson, 1971 ). Les rats apprirent par essais et erreurs qu'ils avaient à presse r, par exemple, huit fois sur le levier A, avant d'appuyer une fois sur le levier B pour ouvrir la porte qui leur donnait accès à la nourriture. Chaque rat avait été formé avec un nombre différent de pressions nécessaires sur le levier A. Pour éviter que les rats pressent sur le levier B souhaité prématurément, les expérimentateurs avaient fait en sorte que l' appareil délivre un léger choc électrique chez le pauvre rat qui se précipitait trop. ( Sans cette configuration, les rats avaient tendance à appuyer sur B immédiatement, à défaut de fournir le nombre requis de  pressions sur A. ) Quoi qu'il en soit, les rats n'ont jamais appris à être précis, parce que, contrairement à nous, ils ne savent  pas compter, ils ne savent qu'estimer le nombre des pressions nécessaire sur le levier A, et leurs estimations, résumées dans la figure 5.2, ont été très révélatrices de ce qui se passait dans leur petit cerveau :

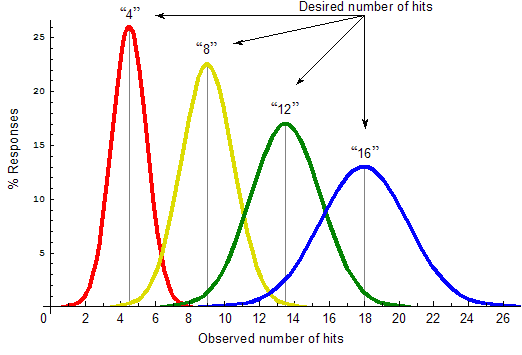
fig 5.2   Performance en numérosité des Rats (adapté de Dehaene, 1997 )

Pour comprendre le graphique de la figure 5.2,  voyons d'abord la courbe rouge. Cette courbe décrit résume ( statistiquement ) les réalisations des rats qui ont appris le nombre "4 " ( vous voyez qu'il est indiqué sur le sommet de la courbe rouge ). La valeur moyenne de cette courbe  sur l'axe des x n'est pas exactement 4 , mais quelque part près de 4,5. C'est parce que les rats ont légèrement surestimé le nombre 4, lors de leur apprentissage : en plus de 4 coups sur le levier A, ils ont donné parfois 5 coups, d'autres fois ( moins fréquemment) 3 coups, de rares fois 6 fois coups, et ainsi de suite. Chaque point de la courbe rouge représente la probabilité qu'un rat donne 2 coups, ou 3, 4, 5, etc. On observe la même tendance avec les autres courbes ( jaune, vert et bleu ), qui résument les estimations des autres rats dans l'apprentissage de nombres différents ( 8, 12 et 16, respectivement ). Nous voyons que dans tous les cas, les rats ont surestimé le nombre de visites : par exemple, ceux qui devaient apprendre «16» ont frappé le levier A 18 fois en moyenne. Ils ont probablement agi ainsi parce qu'ils voulaient " jouer la sécurité " : en raison de la légère décharge électrique, ils évitaient de presser sur B prématurément ; mais d'autre part ils avaient faim, et ils ne voulaient pas continuer de faire pression sur A pour trop longtemps .

En quoi sommes-nous concernés par ces expériences sur les rats ? Parce qu'il est plus facile de réaliser de telles expériences sur eux : tout d'abord, il serait inadmissible de délivrer des chocs électriques à l'homme, et ensuite et surtout, l'homme peut tricher, par exemple, en comptant (9 ) Les observations relatives à la perception de la numérosité, cependant, devraient s'appliquer aussi bien à des rats qu'à des humains. Car la perception de la numérosité n'a rien à voir avec les mathématiques, ni avec notre capacité uniquement humaine à manipuler des nombres comme nous l'apprenons à l'école. Nous partageons le mécanisme par lequel nous percevons la numérosité avec beaucoup d'autres animaux capables de cognition, notamment les rats, oiseaux, dauphins, singes, grands singes, et bien d'autres .

En observant attentivement la figure 5.2 on remarque que plus le nombre qui doit être évalué est grande , moins son estimation est précise, et que la distribution des estimations est donné par une courbe gaussienne. (ou presque : les courbes ne sont pas exactement gaussiennes, mais sont tordues légèrement vers la gauche (même si ce n'est pas ce que montre la figure 5.2), en particulier celles qui correspondent aux plus petits nombres ).

Deuxièmement, il existe des régularités lorsque l'on compare des quantités : lorsqu'on nous  présente en même temps deux boîtes, chacune avec un nombre différent de points,

Plus la différence entre les nombres de points est grande et plus nous discriminons facilement cette différence

En d'autres termes, il est plus facile de discriminer entre 5 et 10 points qu'entre 5 et 6 points. OK, c'est évident. Mais il y a aussi ce résultat :

Plus la magnitude absolue des quantités comparées est petite, plus il est facile de distinguer parmi elles

Cela signifie qu'il est plus facile de distinguer entre 5 et 6 points qu'entre 25 et 26. Évident, aussi, mais seulement quand on y pense un peu...

Les deux observations ci-dessus peuvent facilement être vérifiées sur des sujets humains, qui répondent plus rapidement qu'il y a une différence lorsqu'il est plus facile de distinguer les nombres .

Il est possible que nous utilisions la même capacité pour percevoir les différences de taille entre des formes arbitraires. Considérez la figure 5.3 :

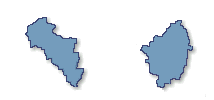
Fig 5.3   Quelle île est la plus grande ?

Dans la figure 5.3, deux îles de la mer Egée sont représentés : Andros sur la gauche, et Naxos sur la droite. Laquelle semble plus grande ? Bien que la recherche sur Internet révèle que Andros ( 374 km2 ) est plus petite que Naxos ( 428 km2 ), on peut arriver au même résultat en se contentant de les regarder attentivement pendant un certain temps. Peut-être y parvenons-nous en nous faisant une idée du nombre de " pixels " qui appartiennent à chaque île ( par exemple, une première discrétisation en « pixels » est assurée par les cônes de nos rétines ), une idée schématiquement représenté sur la figure 5.4 .

Fig 5.4  Discrétisation de la zone des îles ( basse résolution )

Mais quel genre de mécanisme peut expliquer les observations ci-dessus ?

Stanislas Dehaene a introduit la métaphore d'accumulation pour modéliser ces observations ("Dehaene, 1997"). La métaphore d'accumulation dit que quand on vous montre un écran qui affiche par exemple, des points, chaque point n'ajoute pas exactement 1 dans un certain accumulateur de votre cerveau, mais approximativement 1. Plus précisément, c'est une quantité qui a une distribution gaussienne autour de 1 qui est ajoutée. Au lieu de 1, c'est un nombre aléatoire généré à partir d'une distribution gaussienne (" normale" )  de probabilité
N ( 1, σ0 ) qui est ajouté à l' accumulateur. De toute évidence, plus σ0 est petit , plus l'estimation se révélera être précise. Si une personne peut faire de meilleures estimations qu'une autre, c'est probablement parce que l' appareil cognitif de la première personne utilise un σ0  un peu plus petit que la seconde personne. Mais, en fin de compte, ce ne sont que des probabilités, et personne ne peut être sûr de toujours mieux estimer que quelqu'un d'autre. Dehaene dit que cette quantité d '"environ 1 " pourrait être réalisée dans le cerveau par la production d'un produit chimique dont la quantité exacte ne peut pas être réglée avec précision .

Est-ce que la métaphore d'accumulation explique les observations expérimentales ? Oui, et très précisément ! Si vous ajoutez n nombres aléatoires gaussien à partir de N ( 1 , σ0 ), ce que vous obtenez est à nouveau un certain nombre aléatoire gaussien, avec une moyenne μΣ= n et un écart type σΣ = σ0. Ces deux nombres , μΣ et σΣ, déterminent l'emplacement et la forme des courbes de couleur de la figure 5.2, dont les formules sont données ci-dessous ( en fonction de n ) :

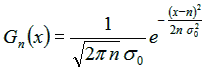
Équation 5.1 : formule pour la perception de la numérosité de n objets.

Ainsi, nous avons une description mathématique des courbes que les rats ( et d'autres animaux, comme les humains ) produisent ( Ceci est bien sûr une approximation : rappelons que pour un petit nombre de la courbe est en fait décalé vers la gauche ; ainsi, l'équation 5.1 permet des nombres négatifs, qui sont bien sûr impossibles, mais, généralement, la correspondance est très bonne. ) La forme de ces courbes ( voir à nouveau la figure 5.2 ) explique pourquoi plus le nombre des entités est petit , plus notre estimation de leur nombre est précise : c'est parce que lorsqu'il y a moins d'objets (n petit ) la courbe de Gauss en cloche est plus étroit e, et il y a donc une forte probabilité que le nombre aléatoire produit sera proche de la moyenne n.

Qu'en est-il de la comparaison des numérosités ? Comment peut-on modéliser mathématiquement les observations sur la façon dont les gens discriminenet rapidement entre les différents numérosités ?

Ces observations peuvent être comprise également grâce à la métaphore d'accumulation ! Si vous avez à faire la distinction entre 5 et 6, vous avez affaire à deux  courbes de Gauss très étroite, avec un faible recouvrement. Lorsque le chevauchement est faible, votre confusion est faible. Mais si vous devez établir une distinction entre 25 et 26, les gaussiennes pour les deux nombres se chevauchent presque partout. Et un chevauchement important signifie une haute probabilité de confusion. OK, la confusion est expliqué qualitativement par les courbes. Mais qu'en est-il des temps de réaction à une discrimination entre les différents numérosités ? Ceux-ci peuvent être modélisés mathématiquement par quelque chose appelé " formule de Welford " ("Welford, 1960 ) :

Équation 5.2  formule de Welford  pour le temps de réaction RT mis à discriminer entre une grande ( L ) et une petite ( S ) numérosité

Le temps de réaction RT dans la formule Welford dépend de L, la plus grande des deux numérosités, et de S, la plus petite des deux, et de quelques constantes, comme a, qui est un léger surcoût initial et représente le temps avant qu'une personne se " réchauffe " assez pour répondre à un stimulus. L'équation 5.2 ne doit pas être interprétée trop littéralement, cependant. Par exemple, si L = S, RT n'est pas définie, ou on peut dire que la formule donne à penser que la personne va attendre à l'infini ( parce que la division par zéro peut être considéré comme la production de l'infini ), évidemment, aucune personne ne sera jamais bloqué e, comme un robot. En général, pour les grands L et S la formule de Welford n'est pas très précis e. Mais, en moyenne elle est assez bonne .

La formule de Welford, proposée en 1960, est une élaboration d'une formule encore plus ancienne, connue sous le nom  de loi de Weber et Fechner ( qui date du19ème siècle ), et qui dit que si le stimulus a une magnitude m, ce que nous sentons n'est pas en soi m, mais une quantité s qui est proportionnelle au logarithme de m, comme ceci: s = k.log (m ) ( k est à nouveau une constante ). Le logarithme explique comment, par exemple, on voit très bien à la fois sous la lumière d'une ampoule, et en plein soleil, dont la luminosité est pourtant des milliers de fois plus supérieure à celle de l' ampoule en termes absolus .

Toutes ces formules sont belles, mais elles ne nous disent pas ce qui est spécial dans la perception humaine de la numérosité, et qui ne se produit pas chez d'autres animaux .

Eh bien, comme d'habitude, la cognition humaine est allé plus loin. Au lieu de percevoir l' ampleur de seulement des quantités discrètes explicites ( comme des points ), l'être humain peut percevoir la magnitude de quantités symboliques. Par exemple, on peut demander à des sujets humains de discriminer en regardant des chiffres tels que 5 et 6, dans leur notation commune (chiffres arabe ), ou de discriminer entre des lettres, tels que e et f , en supposant que chaque lettre correspond à son emplacement ordinal dans l'alphabet. Dans tous ces cas, la métaphore de l'accumulateur et la formule de Welford sont toujours valables. Ceci suggère que toutes les comparaisons de quantités ou de tailles, si abstraite soient-elles, sont régies par les principes de la perception de la numérosité abordés dans cette section .

L'expression "si abstraite soient-elles ", ci-dessus, est cruciale. Par le biais de notre perception de la numérosité nous pouvons avoir une idée de l'ampleur de quantités telles que :

• Combien de fois nous avons mangé de la nourriture chinoise dans la dernière année ( en supposant que nous n'avons pas consommé de la nourriture chinoise sur une base quotidienne, ni que nous avons une certaine aversion pour elle ) .
• Combien de fois le bras fait de va-et- vient lorsque nous nous brossons les dents
• Combien de fois le mot "cognition " apparaît dans le présent document, et si ce nombre doit être supérieur ou pas au nombre d' occurrences de «fondamental » .

Dans aucun des exemples ci-dessus nous ne sommes capables de donner un nombre exact ( dans des circonstances normales ), et nous n'avons pas envisagé de les compter tandis que les événements se déroulaient. Au lieu de cela, nous avons un «sentiment de grandeur », et c'est ce que ce principe affirme .

"

Principe 6: Construction des Association par les co-occurrence (apprentissage Hebbien)

Le fait que les animaux peuvent former des associations est bien connu. En fait, cela peut être considéré comme le résultat le plus solide de la psychologie animale au début du 20e siècle ( cf. les expériences de Pavlov avec les chiens qui salivent après avoir entendu une sonnerie ), et a formé la base de la vue behavioriste stimulus- réponse de la cognition. De nos jours, le point de vue behavioriste a mauvaise réputation dans les sciences cognitives (même s'il a encore des fans avides dans le domaine de la biologie ), parce qu'il échoue à expliquer les observations de la cognition humaine. Pourtant son idée de base transparaît encore dans la cognition, plus précisément dans ce qui est connu sous le nom " d'apprentissage de Hebb », selon lequel, lorsque deux neurones sont physiquement proches et sont activés en même temps, certaines modifications chimiques doivent se produire dans leurs structures et expliquent que les deux neurones émettent ensemble des signaux (Hebb, 1949 ) .

Les psychologues et chercheurs en sciences cognitives ont généralisé cette idée, en affirmant que cela signifie que chaque fois que deux percepts sont perçus ensemble à plusieurs reprises, l' esprit forme une liaison entre eux, de sorte que l'un peut invoquer l'autre. Si elles sont perçues de façon séquentielle, la première peut invoquer la seconde, mais pas le contraire  "; mais si leur perception est simultanée, par exemple, que lorsque nous voyons à plusieurs reprises deux amis apparaître ensemble , la présentation de l'un va invoquer le concept de l' autre. ( Si un seul des amis nous accueille un jour, nous sommes tentés de nous demander ce que fait l'autre. ) Voir la Figure 6.1 pour un exemple bien connu .

Fig 6.1 Quel «ami » M. Hardy suscite dans votre esprit ?

Mais l'exemple qui suit est une " démonstration " du fait que les animaux à créer des associations par co- occurrence. L' autre jour, je me trouvais dans le zoo d'Athènes, en Grèce ( Attique Zoological Park ), à côté de la cage d'un Cacatoès. Les Cacatoès sont des oiseaux semblables à des perroquets, et, comme de nombreux perroquets, ils peuvent apprendre à «parler ». Celui-ci, en plus d'être bon pour parler, était également très friand de caresses. Non, pas seulement friands, il demandait à être choyé par les visiteurs. J'ai inséré un doigt à travers la grille métallique de sa cage et l'oiseau a baissé sa tête charmante, me permettant de caresser son cou et le corps sous l' aile ( qu'il a soulevée, afin que je puisse le caresser là! ). Puis, quand j'ai retiré mon doigt et que je m'apprêtait à quitter, je l'ai entendu dire : " Ti Kanis ? " qui signifie en grec ,  " Comment vas-tu ? " ! - Wow ! Pensais-je, cet oiseau peut parler, aussi ! Je suis donc retourné le caresser un peu plus. Ce scénario se répéta deux fois, et chaque fois  l' oiseau dit : " Ti Kanis ? " alors que je m'éloignais de sa cage. La troisième fois, je me suis dit que je devais l'enregistrer. J'ai demandé à un ami qui était avec moi de tenir compagnie à l'oiseau pendant que je filmais avec mon appareil photo, et quand nous nous sommes éloignés, bien sûr, l' oiseau a laissé échapper un autre " Ti Kanis ? ".

Pourquoi l'oiseau faisait-il cela ? Eh bien, le " Ti Kanis ? " signifiait effectivement pour le cacatoès, " Reviens ici ! ( Je veux plus de câlins! ) "   L'oiseau avait noté, par essais et erreurs, que chaque fois qu'il disait quelque chose cela poussait les visiteurs qui partaient à revenir avec un "wow!", et à lui tenir compagnie un peu plus. L' oiseau a sans doute utilisé cette expression, " Ti Kanis ? ", dès le début, et a associé  son énoncé avec le retour des gens, qui est ce qu'il voulait .

Cet exemple démontre une capacité étonnante pour un animal, que nous attribuons habituellement seulement à des personne. Sur l'ensemble des événements qui se déroulaient pendant que les gens s'éloignaient de sa cage, l' oiseau distingué le cas seul et unique où son " Ti Kanis ? ", avait eu pour effet de ramener les gens vers lui. La première fois que cela arriva, cela avait dû se passer par hasard, vu que le cacatoès n'avait aucun moyen de savoir que le fait de dire quelque chose pouvait avoir un résultat aussi heureux. Simplement, il a remarqué la co-occurrence, peut-être dès la première fois, puis il l'a répété, et s'est finalement persuadé que faisant ceci, il obtiendrait cela. La dernière répétition, qui est toujours un échec ( parce que les gens doivent bien quitter sa cage à un moment donné ) ne lui a pas fait «oublier » l' association. Notre cacatoès m'a rappelé les scientifiques de jadis qui essayaient divers médicaments pour soigner une maladie, et qui en observant que la maladie était bien guérie essayaient de déterminer quel produit chimique avait fonctionné, jusqu'à ce qu'ils arrivent à un "Aha !  bien sûr, c'est cette substance !" Sauf que, ce que nous, humains, pouvons parfois faire avec l'aide de la conscience, et parfois inconsciemment, les oiseaux et autres animaux ne peuvent le faire qu'inconsciemment.

Notez que, jusqu'à présent, l'apprentissage de Hebb peut être considérée comme simplement une autre application du principe de prédiction des objets à partir de leurs parties. Cependant, le sixième principe est en réalité une généralisation de l'apprentissage de Hebb, dans laquelle un percept d'un ensemble donné peut être associé simultanément avec un ou plusieurs percepts d'un autre ensemble, sans que personne ne nous dise explicitement quel percept doit aller  avec lequel. Voici un exemple :

Supposons que vous soyez un enfant, vous avez juste commencé à apprendre votre langue maternelle, de la manière automatique et inconsciente tous les nourrissons procèdent. Vous observez des images du monde - ce que vous voyez - et les mots de votre langue, qui, le plus souvent, se rapportent à des choses que vous voyez, surtout quand les adultes vous parlent directement. Le problème que vous avez à résoudre - toujours automatiquement et inconsciemment - est de savoir quel mot correspond à peu près à ce qui perçu dans votre entrée visuelle. ( Supposons que vous avez atteint un stade où vous pouvez identifier certains mots. ) La difficulté de ce problème réside dans le fait qu'il existe une multitude de percepts visuels à chaque fois, et une multitude de phonèmes linguistiques ( mots, ou d'autres entités morphologiques, tels que les marqueurs du pluriel, possessifs, interjections, et ainsi de suite ). Comment faites-vous une correspondance un-pour-un entre les  mots phonèmes et les objets vus, quand ce qu'on vous donne pour commencer est une relation beaucoup-vers-beaucoup ?

La solution ci-dessous de ce problème fait plusieurs hypothèses qui sont des idéalisations, c'est à dire que le monde réel est plus complexe, mais, comme d'habitude, nous n'arriverons nulle part si nous nous confrontons immédiatement au monde réel dans toute sa généralité. Certaines simplifications doivent être faites, quelques coins doivent être coupés, pour être en mesure de voir d'abord l'idée de base, ensuite, plus de complications peuvent être ajoutés pour vérifier si l'idée de base fonctionne toujours. Donc : supposons que les entrées - à la fois visuelles et linguistiques - vous soit données sous forme de couples comportant une image et une phrase, comme dans la figure 6.2 .

o sheoil eotzifi ot ipits

fig 6.2 : une image (entrée visuelle), et une phrase dans un langage inconnu (entrée linguistique)

"
En regardant l' image, vous pouvez identifier des percepts visuels, tandis que par l'écoute de la phrase, vous pouvez identifier certains signes linguistiques. Mais vous n'avez aucune idée de quel percept visuel peut être associé avec quelle entité linguistique (ou même si une association peut être faite). Donc, étant ignorants comme vous l'êtes, pourquoi ne pas faire une association initiale de tout avec tout ? La figure suivante montre ce genre d'idée :

Fig 6.3. Former des associations entre chaque percept visuel et chaque entité linguistique.

Les percepts visuels sont alignés sur la ligne supérieure de la figure 6.3, et les percepts linguistique sur la rangée du bas, dans aucun ordre particulier ( à souligner qu'il y n'a besoin d' aucun ordonnancement pour que cet algorithme puisse travailler ). Les percepts de l' ensemble visuel ( rangée du haut ) sont supposés être : " maison ", "soleil ", "toit ", " brille ", "cheminée ", et "porte". Notez que ce sont les percepts que vous arrivez à percevoir dans cette présentation particulière de l' entrée, et qu'une présentation de l' entrée à un moment différent pourrait entraîner une perception de percepts un peu différents, mais l'algorithme décrit ici n'est pas sensible à ( est indépendant de ) ces variations dans l'entrée .

Ainsi, chaque percept a été associée à tous les mots dans la figure 6.3, ce qui n'est pas une construction très utile jusqu'à présent, mais le monde continue à vous fournir des paires d'images et de phrases. L'exemple suivant est montré figure 6.4 ."

o sheoil ot eotzifi samanea poa odu onbau
Fig 6.4  Une autre paire d'entrées visuelles et linguistiques

Maintenant, vous avez des percepts visuels différents dans cette image, et des mots (sons) différents dans l'expression. Mais, en général ( de temps en temps ), il y aura un certain chevauchement - vous ne pouvez pas continuer à percevoir des éléments d'entrée différents tout le temps, le monde de votre enfant est fini et limité. Ainsi, les lignes dans la figure suivante (6.5 ) sont censés contenir l'union de votre percepts visuels, et l'union de vos percepts linguistique - au détail prés que, parce que l' espace horizontal sur l'écran d'ordinateur est limité, seul une partie des nouveaux percepts des deux ensembles ( lignes ) est affichée ici :

Figure 6.5. Certains nouveaux percepts visuels et linguistiques sont ajoutés à chaque série (sur les lignes )

Les percepts «montagne », « entre », et « deux » ont été ajoutés sur l'ensemble visuel ( rangée du haut ), et les jetons " Samanea », «poa », et « odu " sur l'ensemble linguistique ( rangée du bas ), dans la figure 6.5. ( tout ce que vous avez perçu, à la fois visuellement et linguistiquement, est supposé être là, on n'a simplement pas tout montré à cause du manque d'espace horizontal. )

Maintenant, nous pouvons faire exactement la même chose que nous avons déjà fait : associer chaque percept de l' entrée visuelle de la figure 6.4 avec tous les apports linguistiques dans la même figure. Le résultat est montré figure 6.6 :

Fig 6.6 Les percepts visuels nouveaux sont associés avec les  nouveaux percepts linguistiques

Qu'est-il arrivé à la figure 6.6 est que certaines des associations d'origine ne semblent pas nouvelles ( la majorité d'entre elles, en fait ), donc la force de ces associations a un peu diminué, automatiquement (représentée en couleur plus claire ). Pourquoi ? Eh bien, supposons que c'est une caractéristique des associations : si elles ne sont pas renforcés, au fur et à mesure que le temps passe, leur résistance diminue. ( Combien de temps ? C'est un paramètre important du système, on le verra plus loin. ) Mais certaines associations (quelques unes ) ont été reprises dans la deuxième entrée, et les associations ont vu leur force augmenter légèrement ( trait plus épais et en couleur foncée ) .

Cette situation se poursuit au fil du temps : plusieurs paires d'images et de phrases arrivent, et les associations qui ne sont pas répétées s'évanouissent, mais celles qui sont répétées dans l'entrée se renforce nt. La figure suivante montre ce processus de  renforcement-décoloration simultané  sur un certain nombre de présentations de paires d'entrée ( image + phrase ) .

Fig 6.7  Une séquence d'animation montrant la création d'associations entre certains percepts visuels et linguistiques

La figure 6.7, ci-dessus conserve le même ensemble de percepts que la figure 6.6. Le lecteur doit supposer que ces ensembles poursuivent continuellement leur croissance, car l' algorithme fonctionne toujours avec  l'union des percepts visuels et l'union des percepts linguistiques. Mais à des fins de visualisation les ensembles de la figure 6.7 ont été tronquées à une taille fixe .

L'essentiel est que, dans la finale des images de l'animation montrée à la figure 6.7 les «bonnes » associations ont été trouvées. J'ai mis "bonnes " entre guillemets parce qu'elles ne sont vraiment correcte que si la correspondance entre les images et les phrases a été cohérente. Mais même si elles sont mauvaises - et certains d'entre elles le sont probablement - temps les réparera : les mauvaises associations ne devraient pas se répéter souvent ( sauf si un professeur maléfique est en cause, mais ici nous supposons une situation normale, dans laquelle les enseignants ne sont ni malveillants, ni particulièrement efficace et capable s, juste l'entrée normale à laquelle les bébés sont généralement confrontés ). Ainsi, ces associations ne sont pas répétées souvent, et même si elles parviennent malgré tout à devenir fort es, elles finiront par s'estomper. Avec assez de temps, seuls les bonnes survivront à ce processus de désherbage .

Pour que l' algorithme ci-dessus puisse vraiment travailler, quelques paramètres supplémentaires et des "interrupteurs de sécurité" doivent être définis. Plus précisément, une fois qu'une association dépasse un seuil suffisant de force, il doit devenir plus difficile pour elle de s'estomper, sinon tout ( toutes les associations ) sera ramené à zéro si les entrées parviennent plus, et l' esprit deviendrait amnésique, oubliant tout ce qu'il a appris. En outre, la manière dont les associations se renforcent et diminuent doit être réglé avec précision en suivant une fonction sigmoïde, illustrée à la figure 6.8 .

Fig 6.8  La fonction sigmoïde selon laquelle les associations se renforcent et s'amoindrissent. 

La fonction a(x), illustrée à la figure 6.8, doit avoir la forme d' une sigmoïde pour les raisons suivantes :

• une augmentation doit être strictement monotone, sinon le mouvement de x le long de l'axe x ne déplacerait pas ( x ) dans la bonne direction .
• La courbe doit être d'abord augmente lentement, de sorte qu'un nombre initial de renforts à partir de x = 0 n'entraîne pas une augmentation brutale de a( x ). Cela est nécessaire parce que si une association est mal faite, nous ne voulons pas un petit nombre de renforcements initiaux se traduire par un  a ( x ) important - nous ne voulons pas que le «bruit » soit pris au sérieux .
• A l'inverse, si x a approche de 1, et donc a( x ) est également proche de 1, nous ne voulons pas que a( x ) chute brutalement vers des valeurs inférieures, a doit être prudente, ce qui signifie qu'une fois qu'un  a( x )  élevé a été établi, il ne devrait pas être trop facile de "l'oublier " .
• Après avoir établi que les parties initiales et finales doivent croître plus lentement, il n'y a que peu de possibilités pour le milieu d'une courbe monotone, d'où la forme sigmoïde de la fonction a.

Tout cela est expliqué plus en détail dans Foundalis et Martinez (2007 ), auquel le lecteur est renvoyé si vous êtes intéressé par les détails. La même publication examine une généralisation de ce sixième principe ( la création d'associations Hebbiennes ) et du premier principe ( catégorisation ) : il est suggéré que le même mécanisme qui est responsable de la catégorisation peut également être responsable de la construction des associations à la mode de Hebbian . Ici, cependant, nous n'avons pas besoin de nous plonger dans cette généralisation, qui, après tout, n'est qu'une possibilité - aucune preuve expérimentale à ce jour ne suggère que le cerveau humain utilise vraiment une procédure générale unique. La généralisation est plus intéressante à des fins de calcul, et de mise en œuvre des agents cognitifs dans un ordinateur : si la nature a été libre - au moyen de la sélection naturelle - d'utiliser n'importe quel mécanisme qui fonctionne, les ingénieurs qui tentent de construire des systèmes cognitifs dans les ordinateurs ne sont pas tenus de répliquer exactement les solutions qu'elle a trouvées .
"

Principe 6 ½: Affaiblissement temporel de la rareté (apprentissage par l'oubli)

Ce principe est numéroté 6½ pour souligner qu'il n'est pas vraiment nouveau, mais introduit un mécanisme plus profond que celui qui figurait déjà dans la discussion du sixième principe. Ce mécanisme, cependant, peut aussi fonctionner indépendamment du sixième principe, et est responsable de certains apprentissages supplémentaire dont nos systèmes cognitifs son capables .

Une fois de plus, supposons que vous êtes un enfant. Des entrée linguistique vous parviennent, principalement dans le discours des adultes. Ce qui vous parvient comme entrée est seulement une fraction minuscule de ce que votre langue maternelle est en mesure de générer, en principe. Par conséquent, vous devez posséder un mécanisme de généralisation qui est capable de générer plus de phrases et  de mots que vous en avez jamais entendu. Par exemple, vous entendez que le participe passé de "saut " est " sauté " , celui de " chatouiller "est " chatouillé ", celui de " rire "est " ri ", et ainsi de suite. A partir de tels exemples, vous devez être capable d'inférer que le participe passé de « caqueter » doit être « caqueté ", même si peut-être vous n'avez jamais entendu la forme " caqueté " avant. De même, vous devez être capable de mettre des mots de façon à faire des phrases que vous n'avez jamais entendu auparavant. ( Cette observation, souvent appelé l'argument de la « pauvreté de l' entrée ", est utilisé comme un argument pour montrer que la cognition humaine doit inclure un mécanisme linguistique inné  capables d'arriver à de telles généralisations, et non pas simplement reproduire ce qui a déjà été entendu. )
"
Parfait. Mais toutes les langues sont délicates. En anglais, par exemple, vous pouvez naturellement conclure que la première personne du verbe « aller»  est « j'alle », et on observe que les enfants font réellement de telles erreurs. La question est de savoir comment les enfants apprennent la forme correcte, " je vais ", si personne ne les corrige explicitement ? Vous pourriez penser que si un adulte entend dire l'enfant : « j'alle », l' adulte va répondre : «Non ! Tu ne dois pas dire « j'alle », tu dois dire « je vais » Mais il y a deux problèmes avec cette idée : d'abord, il a été observé que de nombreux enfants ( peut-être la majorité ) n'apprennent pas en étant corrigés - ils ignorent simplement les corrections. Et en second lieu , corriger le discours des petits enfants est avant tout une habitude occidentale. Il y a des cultures où les adultes ne parlent jamais aux enfants, pensant que l' enfant ne comprendra pas la langue des adultes de toute façon. Dans ces cultures, l' enfant doit apprendre la langue - et réussit à l'apprendre - à partir de toutes les paroles adultes qui atteignent ses oreilles. Dans d'autres cultures, le fait de corriger les enfants n'est tout simplement pas une pratique courante. Alors, comment les enfants parviennent-ils à désapprendre les mauvaises généralisations tort leurs  entrées les conduisent parfois à faire ?

Simple : par le biais du principe 6 ½. Ce principe, qui figurait déjà dans le cadre du principe 6, dit que ce n'est pas un désastre si de mauvais concepts sont formés, ou de mauvaises connexions entre les concepts sont mises en place, parce que le concept ou la connexion erroné est tenu de ne pas se répéter trop souvent dans l' entrée (sinon, il serait bon, pas mauvais ). Ainsi, la mauvaise connexion va s'estomper au fil du le temps ( automatiquement comme expliqué dans le sixième principe ), et le concept erroné deviendra inaccessible, au bout d'un certain temps - et un concept inaccessible est comme s'il n'existait pas. Par exemple, la forme « j'alle » n'est pas celle qui apparaîtra souvent dans l'entrée linguistique de l'enfant - mis à part rarement via d'autres enfants qui auront fait la même généralisation erronée. Ainsi, en supposant qu'il existe un lien qui atteint la forme « j'alle » là où la première personne du verbe «aller » est nécessaire, la force de ce lien s'estomper forcément dans le temps car il n'y aura pas suffisamment de renforcement de l' entrée. Au lieu de cela, la forme correcte " je vais " sera répété plusieurs fois, et l'enfant fera la connexion correcte à un moment donné, perdant éventuellement la capacité d'atteindre la mauvaise formulation « j'alle », parce que la force de la connexion sera trop faible pour qu'une quantité significative d'activation l' atteigne et le sélectionne comme la première personne de "aller " .

Ce qui vient d'être décrit concernant la contribution linguistique se généralise à toute situation dans laquelle nous apprenons l'information en observant des exemples divers, que nous sommes appelés à généraliser pour les utiliser efficacement. La figure suivante montre l' idée générale :

(a)

(b)

"Fig 6.9  ( a) Les deux types exemples positifs et négatifs sont disponibles ; ( b ) Seuls des exemples positifs sont disponibles
"

La Figure 6.9 ( a) montre une situation irréaliste d'apprentissage d'un concept, dans lequel les deux types d'exemples positifs et négatifs sont disponibles. C'est ce qu'on appelle " apprentissage supervisé " dans la littérature, car il est supposé exister un "tuteur " qui sert agent d'apprentissage : « Regarde : c'est un bon exemple de ce que je tente de t'apprendre », puis « Mais maintenant, regarde : c'est un contre- exemple de ce que tu dois apprendre». Ce qui n'est pas réaliste, c'est l'existence du tuteur qui choisit les contre- exemples ( les inconvénients ( - ) dans la figure 6.9.a. ) en plus des effets positifs ( + ). Si un tel tuteur était tout le temps disponible, l' étendue de la notion qui doit être apprise ( bordure en courbe ) pourrait être facilement déterminée. Mais ce qui se passe habituellement dans la réalité,  c'est " l'apprentissage non supervisé ", dans lequel il n'y a pas de tuteur, et aucune confirmation de savoir si ce qu'on a appris est bon ou mauvais. La Figure 6.9 ( b ) ne montre que des exemples positifs ( + ), mais qui, conformément au principe 6 ½, n'ont pas une vie stable. Ceux qui ne sont pas répétés sont souvent - très probablement - les mauvais, et en tant que tels, après avoir "fondu" suffisamment, sont exclus de l' extension de la notion apprise. ( La frontière de la notion est représentée en gris pour refléter le fait qu'elle change de façon dynamique pendant que le concept est appris. )

Notez que ce qui apparaît comme des "+" grisé  dans la figure. 6,9 ( b ) ne sont pas forcément des fausses informations, mais simplement de l'information n'a pas être renforcée dans le passé par la répétition. De cette façon, l'esprit humain conserve toujours les connaissances actuelles. En supposant que la capacité du cerveau humain est finie, si toutes les information étaient conservés indéfiniment, la capacité du cerveau serait dépassée à un moment donné ( probablement au début dans la vie ), et nous nous ne pourrions plus jamais rien apprendre de nouveau. Ainsi, l'oubli est une façon naturelle d'apprendre, plutôt qu'un dysfonctionnement du système de la mémoire humaine .

Principe 7 : Codage et Décodage (CODEC perceptuel)

Les modalités sensorielles ne se bornent pas à percevoir et décoder des perceptions. Elles sont également capables de coder des "pseudo perceptions". Elles fonctionnent comme des codeurs-décodeurs (CODEC). Ceci  permet d'imaginer les variations d'un concept, de penser par exemple à une orange bleue. Et l'imagination est sans conteste un attribut essentiel de la cognition humaine. Ceci permet également de faciliter la compréhension de ce qui est perçu, en particulier si c'est une scène complexe, en comparant le percept avec un pseudo-percept engendré à partir d'hypothèses sur ce qui est perçu : le système sensoriel peut alors se dire "oui ça colle", ou "non, c'est pas ça", ou osciller entre deux versions, comme dans le cas d'illusions d'optiques bien connues sur la profondeur.

Enfin lorsque nous rêvons, les codeurs de nos systèmes percéptuels sont "en roue libre", ils ne sont plus contraints par les sens et peuvent... imaginer ce que nous rêvons.  Certains philosophes soutiennent même que l'esprit rêve en fait en permanence, même lorsqu'il est éveillé, seulement dans ce cas les rêves sont "orientés" par les sensations et deviennent des percepts.  Pour eux, la réalité, c'est du rêve contraint par les sens...

Références : (en cliquant sur le symbole  vous serez ramené là où la référence à été faite)

1. Dehaene, Stanislas (1997). The Number Sense. New York: Oxford University Press. (In Amazon) 

2. Foundalis, Harry E. (2006). “Phaeaco: A Cognitive Architecture Inspired by Bongard’s Problems”. Dissertation Thesis, Computer Science and Cognitive Science, Indiana University, Bloomington, IN. (Download it. Warning: large pdf file (14 MB).)

3. Foundalis, Harry E. and M. Martínez (2007). “A Generalization of Hebbian Learning in Perceptual and Conceptual Categorization”. In Proceedings of the European Cognitive Science Conference, Delphi, Greece, May 2007, pp. 312–317. (Download it)

4. Hebb, Donald O. (1949). The Organization of Behavior. New York: Wiley.

5. Hofstadter, Douglas R. (1995a). Fluid Concepts and Creative Analogies: Computer Models of the Fundamental Mechanisms of Thought. New York: Basic Books. (In Amazon)

6. Hofstadter, Douglas R. (1995b). “A Review of Mental Leaps: Analogy in Creative Thought”. AI Magazine, Fall 1995.

7. Hofstadter, Douglas R. (2001). “Epilogue: Analogy as the Core of Cognition”. In Dedre Gentner, Keith J. Holyoak, and Boicho N. Kokinov (eds.) The Analogical Mind: Perspectives from Cognitive Science. Cambridge, MA: MIT Press/Bradford Book. (In Amazon)

8. Jain, A. K., M. N. Murty, et al. (1999). “Data Clustering: a Review”. ACM Computing Surveys, vol. 31, no. 3.

9. Kruschke, John K. (1992). “ALCOVE: An exemplar-based connectionist model of category learning”. Psychological Review, no. 99, pp. 22–44.

10. Lakoff, George and M. Johnson (1980). Metaphors we Live by. Chicago: University of Chicago. (In Amazon)

11. Mechner, Francis (1958). “Probability relations within response sequences under ratio reinforcement”. Journal of Experimental Analysis of Behavior, no. 1, pp. 109–121.

12. Murphy, Gregory L. (2002). The Big Book of Concepts. Cambridge, MA: MIT Press. (In Amazon)

13. Nosofsky, Robert, M. (1984). “Choice, similarity, and the context theory of classification”. Journal of Experimental Psychology: Learning, Memory, and Cognition, np. 10, pp. 104–114.

14. Nosofsky, Robert, M. (1992). “Exemplars, prototypes, and similarity rules”. In A. Healy, S. Kosslyn, and R. Shiffrin (eds.), From Learning Theory to Connectionist Theory: Essays in Honor of W. K. Estes, vol. 1. pp. 149–168.

15. Nosofsky, Robert, M. and T. J. Palmeri (1997). “An exemplar-based random walk model of speeded categorization”. Psychological Review, no. 104, pp. 266–300

16. Platt, John R. and D. M. Johnson (1971). “Localization of position within a homogeneous behavior chain: Effects of error contingencies”. Learning and Motivation, no. 2, pp. 386–414.

17. Smith, Brian Cantwell (1996). On the Origin of Objects. Bradford Books. (In Amazon)

18. Thompson, Richard F. (1993). The Brain: A Neuroscience Primer. New York, NY: W. H. Freeman and Company. (In Amazon)

19. Welford, A. T. (1960). “The measurement of sensory-motor performance: Survey and reappraisal of twelve years progress”. Ergonomics, vol. 3, pp. 189–230.

Notes : (en cliquant sur le symbole  vous serez ramené là où la note  à été citée)

1. Dans l'expérience des deux fentes, les particules créent - ou ne parviennent pas à créer - une figure d'interférence sur un écran derrière un diaphragme avec deux fentes ouvertes - ou  seulement une fente ouverte.[ ](http://sboisse.free.fr/science/psy/principes-perception.php#ancre1)
2. Bien que mes "points" apparaissent comme des petits disques,  leur taille ne compte pas.  J'aurais pu les tracer comme des pixels uniques, mais vous auriez eu besoin d'une loupe pour voir ce que contient la figure
3. Il n'y a pas que les humains qui peuvent faire cela : plusieurs sortes d'animaux perçoivent effectivement deux groupe de points, comme cela a été démontré lors d'expériences en laboratoire. [ ](http://sboisse.free.fr/science/psy/principes-perception.php#ancre_note2)
4. En effet, de nombreux algorithmes dits de classification ou de "clustering" sont connus (Jain, Murty et al., 1999). Les gens (et les animaux) n'utilisent bien sûr pas les coordonnées x et y, mais leurs systèmes visuels sont capables de calculer les distances entre les lieux, et c'est tout ce qui est nécessaire pour résoudre ce problème.
5. La Figure 1.3 est une exagération. En réalité, la rétine possède des millions de cônes et des bâtonnets, qui peuplent très densément une zone appelée la fovéa, correspondant au centre du champ visuel de chaque œil, et plus faiblement  la région environnante
6. L'analyse multidimensionnelle peut nous dire quelles sont, parmi toutes les dimensions possibles, celles qui ont été utilisées dans la tâche de catégorisation, mais elle ne nous dit pas comment arriver à l' ensemble de toutes les dimensions possibles, en premier lieu
7. "Il est bien connu que les petits enfants font souvent des phobies du type crocodile- sous-le- lit : il pourrait y avoir un crocodile se cache sous le lit , ou dans un placard, mais qui disparaît comme par magie si l' enfant ose  inspecter cette zone. Toutefois, c'est probablement un effet secondaire de la cognition complexe et de la riche imagination que les petits enfants possèdent généralement, et je pense qu'il est très peu probable que tout animal possède les aptitudes cognitives pour concocter de telles prouesses d'imagination
8. Une fois j'ai vu un petit chat jouant avec un coléoptère. Le coléoptère marchait sur la surface supérieure d'un mur de ciment, sur laquelle le chat était assis, et je les regardais d' un balcon, plus haut. Le scarabée tentait désespérément de s'échapper, mais le chaton bloquait son chemin, le faisant changer de direction tout le temps. Après  environ une minute ou deux ce ce petit jeu, le chaton finit par s'ennuyer et laissa  le scarabée partir. Si ce n'est pas un exemple d'un animal jouant avec un jouet, alors je ne sais pas ce que c'est
9. Pourquoi voulons-nous pas compter ? Parce que le comptage est une capacite complètement différente, une capacité que seul l'homme possède, et que nous ne possédons pas à la naissance, mais apprenons laborieusement dans notre enfance. Le comptage se rapporte à l'arithmétique, mais pas la perception de la numérosité ; le premier exige de passer par l'école, la dernière est spontanée.

NOTE de Serge Boisse :
Avant de découvrir le texte de Foundalis ci-dessus, j'avais tenté (en 2004) de décrire les "lois de l'humanotique", des lois régissant l'être humain, à la manière des fameuses "lois de la robotique" d'Asimov. Mais Foundalis est bien plus clair et bien plus précis, au moins sur les modalités sensorielles.  Les deux textes sont donc complémentaires.
Enfin, si vous vouslez en savoir plus sur le fonctionnement de l'esprit humain, allez voir ici !