Journal d'un Terrien
Web log de Serge Boisse
On line depuis 1992 !
http://sboisse.free.fr/science/cosmologie/cosmo_maths.php
Cosmo Maths !
La science moderne a la réputation de se construire à partir de calculs affreusement compliqués que seules les grosses têtes peuvent comprendre. Mais les idées fondamentales sont toujours très simples, et il est fréquent que l'on puisse les justifier de manière parfaitement valable à l'aide calculs qui ressemblent à des calculs d'épicier.
Les notes qui suivent sont des exemples dus à Jean-Pierre Petit, de l'observatoire de Marseille.
Comment retrouver les lois d'évolution de l'univers en trois lignes de calculs
Assimilons l'univers à un grumeau homogène de poussière de rayon R et de masse M. Considérons un grain de poussière de masse m situé à sa surface. Newton a montré que la force qui s'exerce sur cette masse est la même que celle que produirait toute la masse M concentrée au centre O, c'est à dire :
Appliquons
Il vient :
Construisons l'une des trois solutions de cette équation différentielle : donnons pour ce faire à la fonction
R(t) est la longueur caractéristique de cet univers, qui peut être assimilé à son rayon de courbure, ou encore à la distance moyenne entre deux particules :
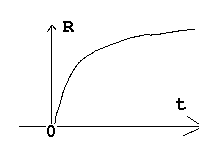
L'univers autistique
Un simple coup d'oeil à la courbe R(t) montre que l'expansion de l'univers a commencé par une explosion, la vitesse d'expansion allant ensuite en se ralentissant. Si l'on assimile R(t) à la distance moyenne entre deux particules, ct représente le rayon d'une onde électromagnétique émise à l'instant t=0. Avec une vitesse de la lumière constante, on voit que le rayon de cette "sphère horizon", ou sphère du connaissable restera pendant un certain temps inférieur à la distance moyenne entre les particules, lesquelles s'ignoreront totalement pendant cette période.

Et voilà pourquoi l'univers primitif était non collisionnel !
Comment calculer le rayon d'un trou noir
Soit un astre de rayon
Cette énergie excédera l'énergie maximale disponible si
En fait, un calcul plus fin tenant compte de la diminution de la masse conduirait à
Si une masse
Mais un photon ? Le photon a une énergie
Les conditions de Planck
La dimension spatiale d'une particule (sa taille) est donnée par la longueur d'onde de Compton
Supposons que cette particule soit un trou noir : Alors cette longueur
Soit alors un photon de longueur d'onde
Quand la longueur d'onde d'un photon égale son rayon de schwartzchild, il se met à tourner en rond comme un serpent qui se mord la queue et l'information ne peut plus circuler. A cette longueur est associé le temps
La super-relativité ou la théorie de jean-pierre Petit
Il est conseillé de lire la page que j'ai écrite sur les paradoxes de la cosmologie
On "rend leur liberté" à toutes les "constantes" de la physique. Par exemple
MAIS ce sont des constantes ! On ne pas peut pas les faire varier !
FAUX, car on peut les faire varier toutes en même temps en conservant entre elles des relations précises :
Dans l'équation de la relativité générale d'Einstein, la constante
Donc
On suppose que l'énergie
On suppose que les galaxies, le système solaire, les trous noirs, les protons et les neutrons "grandissent" en même temps que l'univers, dont le périmètre est pris égal à
Comme par ailleurs
Prenons maintenant deux étoiles de même masse
L'extension spatiale du proton étant donnée par sa longueur d'onde de Compton
La résolution de l'équation d'Einstein, en supposant l'univers homogène et isotrope (métrique de Robertson-Walker) conduit à l'équation différentielle suivante :
L'horizon cosmologique se définit par l'intégrale
On trouve
L'entropie devient S ~ Log t. Dans une description où l'entropie remplace la variable temps, la singularité initiale disparaît :

On peut se demander d'ailleurs s'il ne serait pas possible de trouver une substitution analogue pour les variables d'espace ?
Toutes les équations de la physique (boltzmann, schrödinger, Maxwell) sont invariantes par les transformations obtenues. De plus on trouve que le red shift est proportionnel à la distance (loi de Hubble).
Comment vérifier la théorie ?
Jusqu'à quelques milliards d'années -lumières les distances calculées pour les sources sont quasiment identiques aux distances issues du modèle standard. L'énergie des photons
En 1988, Bartel et Miley (Nature, vol 373 may 1988) on montré que plus les quasars étaient loin, plus ils étaient petits. Ceci cadre avec la théorie, où les quasars "grandissent" avec l'univers lui-même.
La théorie de JPP n'est pas achevée : il reste à voir comment faire varier certaines constantes liées aux processus nucléaires. Pour le moment, elle ne contredit aucune observation et permet de régler les cinq paradoxes de la cosmologie "orthodoxe" :
Les cinq paradoxes
La théorie de Jean-Pierre Petit (dit JPP) est désormais achevée et porte le nom de théorie Janus. Elle est bien plus complexe que la théorie simpliste que j'énonce dans cette page.
Cependant, cette théorie est bizarrement systématiquement dénigrée par le corpus scientifique français et n'a trouvé jusqu'ici qu'un faible écho.
OK, ça a l'air d'une théorie du complôt. Mais pour une fois, je pense que ce n'en n'est pas une. Je crois que JPP a raison.
Le principal résultat de JPP est le suivant :
La théorie JANUS
Auteur: Serge Boisse
Date: Le 24/03/2023 à 17:03
Type: web/MOC
tags:
- cosmologie
- relativité
- physique
pub: oui
commentaires: ouiLa théorie JANUS

Ce modèle cosmologique dû à Jean-Pierre Petit est une extension de la relativité générale. Il est bimétrique : il y a deux deux univers (2 feuillets topologiques en pratique), liés uniquement par la gravitation, avec une constante de couplage négative.
Les deux univers partagent le même espace-temps et sont liés uniquement par la gravitation. Ce qui fait que les masses situées dans "l'univers jumeau" sont invisibles et indétectables sauf par leurs effets gravitationnels.
IL n'y a pas de masse négative, c'est seulement la constante de couplage qui l'est : Les masses de chaque univers s'attirent entre elles. Les masses d'un univers repoussent celles l'univers jumeau. Il n'y a pas d'effet "run-away".
D'où les deux métriques :
et
On peut comparer avec l'équation de champ d'Einstein :
Ainsi le modèle Janus fait disparaître la constante cosmologique
Cette théorie est compatible avec l'intégralité des observations physiques et astronomiques à ce jour (2025) Mais à la différence de la théorie des cordes qui est stérile, la théorie Janus prédit des phénomènes nouveaux. D'ailleurs certains de ces phénomènes ont déjà été observés mais non remarqués comme étant des conséquences de la théorie. Citons par exemple la très fameuse matière noire, dont la théorie Janus n'a nul besoin.
cf https://www.nexus.fr/wp-content/uploads/2017/03/Le_Modele_Cosmologique_Janus-JPPetit-2016.pdf
et https://www.agoravox.fr/tribune-libre/article/modele-janus-de-jean-pierre-petit-201625
Si cette théorie n'est pas connue de la plupart des physiciens, c'est en raison du caractère parfois irascible de son auteur, qui a tendance à s'emporter violement contre tous ses détracteurs, parmi lesquels quelques scientifiques de grand renom et qui n'ont pas apprécié ce traitement. Il est vrai aussi qu'ils avaient parfois raison... mais pas toujours, la théorie Janus en est la preuve.
Si les questions mathématiques liées à la cosmologie vous intéressent, allez donc voir mes recherches mathématiques personnelles !
Commentaires (0) :
Page :Ajouter un commentaire (pas besoin de s'enregistrer)
En cliquant sur le bouton "Envoyer" vous acceptez les conditions suivantes : Ne pas poster de message injurieux, obscène ou contraire à la loi, ni de liens vers de tels sites. Respecter la "netiquette", ne pas usurper le pseudo d'une autre personne, respecter les posts faits par les autres. L'auteur du site se réserve le droit de supprimer un ou plusieurs posts à tout moment. Merci !Ah oui : le bbcode et le html genre <br>, <a href=...>, <b>b etc. ne fonctionnent pas dans les commentaires. C'est voulu.