Auteur: Serge Boisse
Date: Le 24/03/2023 à 18:03
Type: web/MOC
Tags: 
pub: oui
commentaires: ouiCopier

Le modèle standard... et ses problèmes

Donc il y aurait eu un big bang. Quand donc ? Cela dépend du rythme d'expansion de l'univers. Il est probable que ce rythme se ralentit avec le temps, car l'attraction gravitationnelle entre les galaxies, la masse de l'univers lui-même, en fait,  "freine" l'expansion. 

La constante de Hubble, qui relie la vitesse de récession (d'éloignement) des galaxies avec leur distance, nous permet de donner un âge maximum pour l'univers :

Dans cette figure, qui représente le "rayon" de l'univers en fonction du temps, la pente de la droite tangente au point "maintenant" est donnée par (l'inverse de) la constante de Hubble. L'âge de l'univers est égal aux 2/3 de celui qu'on trouverait en prolongeant la droite. Le problème, c'est que la mesure de cette "constante" est très difficile. Elle a d'ailleurs été réévaluée plusieurs fois.
Mais on estime que l'univers aurait environ 15 milliards d'années. Rappelons que cette mesure suppose que la constante de Hubble est bien constante (dans l'espace et dans le temps), ce qui n'est pas établi formellement...

Big crunch ?

Cet âge vénérable est cohérent avec celui des plus vieilles étoiles, que l'on peut calculer grâce aux modèles internes de leur fonctionnement nucléaire (Ce serait un comble que l'on trouve des étoiles plus vieilles que l'univers... et en fait on a cru plusieurs fois qu'on y était arrivé, mais à chaque fois on a dû déchanter).

Quid du futur de cet univers ? L'expansion va-t-elle continuer indéfiniment, ou bien s'arrêter, auquel cas elle sera suivie d'une phase de contraction de plus en plus accélérée, conduisant finalement à un "big crunch", l'inverse du big bang ? Cette dernière hypothèse ne manque pas d'attraits : selon certains théoriciens, lors de la contraction, le temps "s'inverserait" conduisant à un modèle séduisant, géométriquement simple. On peut aussi imaginer que le "big crunch" serait suivi immédiatement d'un nouveau big bang, une sorte de rebond. On aurait alors un univers cyclique, avec des phases d'expansion puis contraction, séparées par des big bang/cruch. Lors de ces dernières, toute l'information sur la structure de l'univers serait perdue : aucune information ne pourrait passer d'un univers à l'autre. Nous n'avons donc aucun moyen de savoir comment était l'univers qui aurait précédé le nôtre...

Il faut dire aussi que le big bang correspond à la création de l'espace-temps : ce n'est pas seulement de l'énergie qui est créée, mais aussi l'espace et le temps eux mêmes. Ainsi la question de savoir ce qu'il y avait "avant le big bang" n'a pas de sens. Mais avant de préciser ce que cela veut dire, restons dans notre univers : alors, big crunch, ou pas ?

Tout dépend de la densité moyenne de l'univers. Si cette dernière est supérieure à une certaine densité critique (très faible : quelques atomes par mètre cubes), alors l'expansion s'arrêtera et on aura finalement droit au big crush (dans une centaine de milliards d'années, y a pas le feu): on dit que l'univers est fermé. Si cette densité est inférieure ou égale à la densité critique, l'expansion se poursuivra indéfiniment : on dit que l'univers est _ouvert.

_Or il est possible d'évaluer la densité moyenne de l'univers :  On calcule tout d'abord celle des galaxies (facile, puisqu'on connaît leur taille et la masse des étoiles et des nuages interstellaires qui les composent), puis la densité moyenne des galaxies dans l'univers : Celles ci semblent  regroupées en amas, de quelques dizaines ou centaines de galaxies, et ces amas sont eux-mêmes groupés en "super amas", qui... ne sont pas regroupés en super-super amas, eh non, désolé de vous décevoir. Les super amas semblent être les plus grandes strctures de l'univers. Ils sont disposés en longues bandes, des sortes de "filaments", un peu comme des toiles d'araignées, séparés par des vides immenses. Au total, le résultat est inférieur à la densité critique : il semble que l'expansion de l'univers doive se poursuivre sans fin.

Voire. Car dans ces calculs on ne prend en compte que la matière visible . Or il semble bien qu'il existe une foultitude d'objets invisibles dans l'univers : les trous noirs, les neutrinos, les planètes solitaires, et la "matière sombre". Voilà autre chose. Qu'est ce que c'est que ces trucs la ? Je vous parlerai plus loin de ces objets insolites. Pour le moment, ce qui nous occupe, c'est que la densité de l'univers pourrait être supérieure ou égale à la densité critique. Pour des raisons esthétiques (mais si), les cosmologistes aimeraient bien qu'elle soit pile égale à la densité critique, mais on est là en pleine spéculation. Prendre ses désirs pour des réalités n'a jamais fait avancer le schmilblick... Mais la situation n'est pas si simple.

La courbure de l'univers

La topologie, c'est l'étude des formes. Quelle est la "forme" de l'univers" ?. On l'imagine toujours comme une sorte d'immense sphère. Mais ce n'est pas la réalité ! D'abord on ne peux pas séparer l'espace et le temps : nus vivons dans un espace-temps. Et cet espace temps est courbe. Ouh la ! Ça y est, le mal au crâne commence. Pour comprendre vraiment cela, il faut  de solides notions de relativité . Mais ici, je vais essayer (attention, j'ai bien dit : essayer) de faire simple.

L'espace ordinaire dans lequel nous nous imaginons que nous vivons possède trois dimensions : cela veut dire simplement que pour  repérer la position d'un objet à parti d'un autre objet "origine", pris comme référence, il nous faut 3 coordonnées, trois nombres, que nous appellerons x,y,et z. La distance d entre un objet et l'origine peut se calculer simplement grâce au théorème de pythagore : elle est telle que d2 = x2 + y2 + z2. On l'appelle la distance Euclidienne (du nom d'Euclide, un savant grec de l'antiquité) et on dit que l'espace est euclidien.

Mais l'espace-temps  de la relativité n'est pas euclidien, et de plus il est  à quatre dimensions :  cela signifie simplement qu'il nous faut une quatrième coordonnée, que nous appellerons ici q, pour positionner un objet par rapport à un autre. Mais q n'est pas le temps, comme on pourrait le croire. En réalité on a q = i.c.t, où t est le temps, c la vitesse de la lumière et i un nombre "imaginaire" tel que i2 = -1. Dans un tel espace, les points sont des évènements : ils correspondent à "ici et maintenant" ou "là bas et à telle date". En relativité, on aime bien appeler s (et non plus d) la distance entre deux points-évènements. Et on obtient s2 = x2 + y2 + z2 - c2t2 (noter le signe moins). On peut se représenter un tel espace en imaginant que la coordonnée q = ict mesure les intervalles de temps en "mètre de temps". Un mètre de temps, c'est la durée qu'il faut à la lumière pour parcourir un mètre. La "distance" s définie ci dessus s'appelle la distance de Minkowski. En relativité, on l'appelle "temps vécu" ou "temps propre".

Lorsque les mathématiciens définissent une distance, ils cherchent les transformations qui conservent cette distance. Dans l'espace ordinaire, euclidien, ces transformations sont les translations et les rotations. Dans l'espace "Minkowskien" de la relativité, ces transformations se réduisent à une seule : la transformation de Lorentz , qui correspond à une "rotation d'un angle imaginaire" du système de coordonnées à quatre dimensions...

Mais ce n'est pas tout : On nous dit que cet espace-temps est courbe. Qu'est ce que cela signifie ? Voici une façon très simple de se le représenter : imaginons que l'on cherche à atteindre une cible située à 10 m de nous avec un ballon et avec une balle de fusil. Dans l'espace ordinaire, les trajectoires, représentées ci contre, sont très différentes. Avec un ballon lancé à 10 m/s, on peut atteindre la cible en faisant décrire au ballon une arche de 3m de hauteur, et le parcours du ballon durera une seconde et demie. Avec un fusil, qui tire des balles à 500 m/s, on peut attendre la cible avec un tir très tendu, faisant une arche de 0,5 mm de hauteur, et une trajectoire qui durera deux centièmes de secondes ; ou bien, en tirant presque verticalement, on peut faire faire décrire à la balle une arche de 12 Km de hauteur : notons qu'il faut être très bon tireur, et que l'on néglige les effets atmosphériques et la rotation de la terre !

A la limite, on peut atteindre la cible avec un photon de lumière, lancé à 300000 km/s. l'arche (qui existe bel et bien) est alors totalement imperceptible, le tir est quasiment rectiligne.

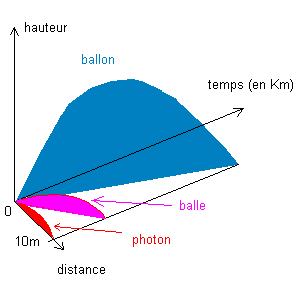Mais ajoutons la dimension temporelle et mesurons le temps en mètres de temps (figure ci-contre). Les courbures des trajectoires deviennent toutes les mêmes , que ce soit pour le photon, le ballon ou la balle de fusil. Ce rayon de courbure est gigantesque : le centre de courbure se trouve presque à une année lumière ! Cette courbure uniforme, c'est celle qui est engendrée par la gravité terrestre : La matière courbe l'espace-temps, d'autant plus que cette matière est dense.

C'est la raison profonde de ce fait qui avait stupéfié Gallilée : l'accélération d'un corps en chute libre (un kilo de plume ou une tonne de plomb) est toujours la même au voisinage de la terre : 9,8 m/s2, ou 1G. La relativité nous dit que c'est la courbure de l'espace-temps, due à la masse de la terre, qui crée cette accélération que nous appelons la pesanteur.

Naturellement, le centre de courbure de la gravité terrestre, situé à une année-lumière "sous" le sol, ne se situe pas dans l'espace tridimensionnel, de même que le centre d'un cercle ne se situe pas sur le cercle.

Et l'univers, qui contient de la matière, est -il courbe ? Et bien non ! Sa courbure moyenne semble absolument nulle, d'après les observations. Voilà un fait curieux, qui mérite qu'on s'y attache un peu.

Quelle est donc la "forme" de cet univers  ?

Imaginons une surface à deux dimensions, plongé dans un espace à trois dimensions : et imaginons que cette surface ait une courbure nulle en tout point. Vous penserez alors que cette "surface" ne peut être qu'un plan. Faux ! Il existe de nombreuses  "surfaces à courbure minimale" et elles sont loin d'être planes ! Il faut voir que lorsqu'on parle de courbure nulle, ce que l'on appelle courbure est la somme des courbures locales dans toutes les directions : si vous imaginez une selle de cheval, par exemple, elle est courbée à la fois vers le haut (vers le pommeau) mais aussi vers le bas (vers les étriers) dans une direction perpendiculaire. Globalement; la selle de cheval est une surface à courbure moyenne nulle.

Or il se trouve que, en quatre dimensions, la géométrie n'est pas du tout intuitive : les "surfaces à courbure minimales"  sont nombreuses. L'univers n'est peut-être pas simplement une "hypersphère". Il se peut que sa "forme" soit bien plus compliquée. Il se pourrait que la vraie forme de l'univers soit un "revêtement à deux feuillets d'un 4-tore", dans le langage imagé des mathématiciens. La vraie réponse est : on ne sait pas. En fait, on ne sait même pas si l'univers est fini ou pas (c'est à dire s'il possède des "branches infinies", puisque tout dépend du rapport entre sa densité et la fameuse "densité critique".

En réalité chaque cosmologiste a ses préférences ! Les équations de la relativité générale peuvent conduire à plusieurs solutions, statiques ou en expansion, pour la forme de l'univers. En réalité, elles ne nous permettent pas de trancher. C'est l'observation qui le permettra. Il se pourrait qu'on observant le ciel très profond, les galaxies les plus lointaines, on observe en réalité notre voisinage (tel qu'il était il y a 15 milliards d'années, du moins), parce que les photons émis par les galaxies auront fait "le tour de l'univers". Comme la terre qui est ronde, l'univers n'a pas de "bord". Il peut être tout à la fois fini et infini.

Mais en fait il existe un "bord" : un horizon dans le passé. Tout ce qui se situe moins de 300 000 secondes après le big bang nous est invisible, parce qu'avant cette date l'univers était non-collisionnel : il se dilatait si vite qu'aucune interaction entre les particules n'était possible (voir cosmo maths sur ce site). Après cet instant clef, les particules purent enfin interagir et les photons s'échapper de la fournaise. Le rayonnement de fond cosmologique (voir la page précédente ) date de cet instant. Et les mesures que l'on peut faire de ce rayonnement montrent que l'univers était formidablement homogène à cette époque : sa densité moyenne varie de moins de 1/10000e dans toute la sphère céleste.

D'où, trois questions fascinantes :

• Si l'univers primitif était non collisionnel, comment a-t-il pu être aussi homogène, au moment où il a émis le rayonnement cosmologique ? Lors d'une explosion "normale", par exemple celle d'une grenade ou d'une bombe atomique, on observe toujours de fortes disparités dans les débris : ils ne s'en vont pas uniformément dans toutes les directions ! Pourtant le big bang a été une explosion pratiquement uniforme, alors même que les constituants de l'univers primitif ne pouvaient pas interagir entre eux ! Et puis, la question qui tue : pourquoi, actuellement, observe-t-on une courbure nulle, alors que la densité de l'univers primitif était forcément énorme, et donc sa courbure ne pouvait pas être nulle ?
• L'univers primitif (300000 secondes après le big bang était uniforme.. mais pas complètement : Pourquoi donc ces déséquilibres infimes (1/10000e) ? Qu'est ce qui les a causé ?
• Notre univers aujourd'huiest loin d'être uniforme ! Comme on peut l'observer de nos jours, les super amas de galaxies se répartissent en longs filaments séparés par des vides immenses. Comment donc des disparités infimes ont-elles pu s'amplifier ainsi pour créer ces immenses structures, et pour créer les galaxies ? D'ailleurs, quelle est l'origine des galaxies ?

L'inflation

La théorie en vogue pour expliquer le premier fait est celle de l'inflation : On imagine que, juste après le big bang, disons une seconde après, de fortes disparités existaient dans l'univers. Mais, moins d'une seconde plus tard, l'univers se serait dilaté si vite que ces disparités auraient été aplanies et que l'univers serait devenu quasiment "plat". Il faut bien voir que l'on parle d'une dilatation quasi instantanée de la "bulle d'univers", dont le volume aurait augmenté d'un seul coup des milliards de milliards de fois ! Cela semble complètement ad-hoc et farfelu. Pourtant les physiciens qui étudient les "champs scalaires" on déterminé que des instabilités de ces champs pourraient causer une inflation telle que je viens de la décrire. Cette théorie, parce qu'elle est plausible, a été bien reçue par les cosmologistes dont la majorité pensent qu'il y a bien eu une "ère inflationniste", peu après le début de l'univers.

Mais en fait on est dans le domaine de la spéculation pure. En réalité, les problèmes de l'homogénéité de l'univers primitif et de la platitude de l'univers actuel demeurent.

La constante cosmologique

Au début de ce siècle, Einstein s'attache à comprendre la structure de notre Univers et, en examinant ses équations, découvre que celui-ci est en expansion. Refusant d'admettre cette idée (à l'époque, tout le monde croyait que l'Univers était statique), le physicien invente une « constante cosmologique » destinée à contrebalancer cette expansion. En ajoutant cette constante au terme de l'équation qui décrit la matière, il permet à l'univers d'être plat.

Bien vite cependant, la constante cosmologique disparaît des équations, dès que la communauté scientifique accepte l'idée que l'Univers est bel et bien en expansion. (Einstein répétera plus tard que la constante cosmologique aura été la plus grande erreur de sa carrière!). Donc elle vaut zéro. Pendant des années, on l'oublie.

Mais la situation n'est peut-être pas aussi simple. En observant des supernovae très lointaines, à la fin de l'année 1998, une équipe internationale de chercheurs a calculé que non seulement l'Univers est en expansion, mais il connaîtrait une phase d'accélération depuis environ 4 milliards d'années! Pour expliquer ce phénomène, la constante cosmologique doit reprendre du service : Cette fois, elle symboliserait « l'énergie du vide », dont la force serait de sens opposé à la force gravitationnelle. Si le phénomène d'accélération est confirmé, ce résultat changera quelque peu notre vision du monde...

Il faut bien voir que l'introduction de la constante cosmologiques dans les équations ne repose sur aucune justification  théorique :  La relativité sans la constante cosmologique est une très belle construction théorique qui repose sur un principe universel, le principe de relativité : les lois de la nature doivent garder la même forme dans tous les référentiels utilisées pour les décrire. Mais la constante cosmologique a simplement été "ajoutée là" pour que les équations permettent à l'univers d'être en expansion. Aujourd'hui, on cherche (et on trouve) des arguments provenant de la mécanique quantique pour "justifier" l'introduction de cette constante : En mécanique quantique, le vide possède une énergie. Il en résulte une force de "pression" négative qui s'exerce sur l'espace lui-même, qui doit donc se dilater. Le problème, c'est que ce mélange de la théorie quantique et de la relativité générale se fait mal.

Certains théoriciens (rares) refusent d'admettre la constante cosmologique et pensent qu'il faut repartir des principes fondamentaux et de la géométrie. La relativité est une théorie géométrique, c'est dans la géométrie, dans la topologie de l'univers, que l'on doit trouver la solution. Hum hum !

Antimatière

Mais au fait, les lois de la physique permettent à deux "sortes de matière" d'exister : la matière et l'antimatière. Elles différent entre elles par la charge électrique et la "parité" (voir les pages "physique" de ce site pour plus de détails). Lorsque une particule de matière et une particule d'antimatière se rencontrent, elles s'annihilent mutuellement dans une gerbe de rayonnement gamma. De même à l'inverse, un photon gamma suffisamment énergétique peut se transformer spontanément en un couple particule (par exemple un électron)  PLUS antiparticule (ici un antiélectron, ou positon). Le photon, lui, est sa propre antiparticule, ce qui est bien pratique pour survivre.

 Or il se trouve que la terre, le système solaire, notre galaxie, tout l'univers connu en fait, est formé de matière, et non d'antimatière. Comment le sais-t-on ? très simple : Les collisions de galaxies, ça existe : C'est un évènement rare mais, vu le nombre de galaxies dans l'univers, on peut en observer facilement des tas. Et s'il existait des antigalaxies, leur rencontre occasionnelle avec des galaxies "normales" produirait un tel barouf radio qu'on l'entendrait jusqu'à l'autre bout de l'univers. Or ce vacarme, on ne l'entend pas.

La où le bât blesse, c'est qu'il n'y a aucune raison pour que le big bang ait produit plus de matière que d'antimatière. En fait le modèle standard nous dit que ces quantités étaient presque égales, à un milliardième près. Et lorsque l'univers est devenu collisionnel, il a échappé de bien près à l'auto destruction complète. En fait il ne reste plus du tout d'anti matière, et un milliard de fois moins de matière qu'il n'y en avait à l'origine. En revanche l'univers actuel contient un milliard de fois plus de photons que de particules de matière. Mais pourquoi y a avait-il un petit milliardième de matière en plus ? Très bonne question...

Ça ne tourne pas rond...

Résumons nous :

• Il y a quinze milliards d'années, le big bang : non pas une explosion dans l'espace, mais une création de l'espace-temps, qui a eu lieu partout à la fois, dans un univers dont la taille était moindre que celle d'une particule et la densité fantastiquement élevée. L'origine du big bang elle même est un mystère. Fluctuation quantique, nous dit-on. Hum !
• Au bout de moins d'une seconde, phase d'inflation (hypothétique)  : multiplication par un nombre astronomique des dimensions de l'univers, en un temps quasi instantané, à cause d'instabilités de certains "champs scalaires". L'inflation cesse aussi brusquement qu'elle a commencé et l'univers poursuit son expansion à un rythme "normal". L'univers est alors une "soupe" extrêmement chaude de particules élémentaires et de photons , mais bien plus homogène qu'auparavant.
• A t=300 000 secondes, l'univers devient collisionnel : il s'est suffisamment refroidi pour que les photons puissent s'échapper librement. L'univers est alors remarquablement homogène (au 1/10000e près).  Matière et antimatière peuvent désormais se rencontrer, et  se détruire mutuellement et joyeusement, ce qu'elles ne manquent pas de faire. Il ne reste que des photons, et un petit milliardième de matière.
• Des quantités colossales de photons qui furent émis alors, il reste aujourd'hui encore la trace : le rayonnement cosmologique, qui est celui d'un corps noir à 3°Kelvin. Les premiers atomes se créent, car protons, neutrons et électrons peuvent désormais s'unir. L'univers est alors formé uniquement d'hydrogène (80%) et d'hélium (20%). Il ne contient aucun atome d'une autre sorte !
• Moins d'un milliard d'année après le big bang, la structure à grand échelle de l'univers se dessine et les premières galaxies commencent à se former. L'univers se dilate toujours, mais de moins en moins vite. Comment les très faibles fluctuations de l'univers primitif ont-elles pu s'amplifier au point de dessiner un univers fait de vide et de matière séparés par des espaces immenses, mystère.
• Cinq a dix milliards d'années après le big bang, les galaxies sont toujours là. En leur sein, les étoiles de première génération, arrivées au bout de leur vie, explosent l'une après l'autre, et dans ces fantastiques explosions les protons fusionnent, de nouveaux atomes se créent : Carbone, Oxygène, Fer..., enrichissant l'espace alentour en éléments lourds qui forment des nuages immenses, puis se condensent lentement et seront captées par les étoiles de seconde génération, dont notre soleil.
• Aujourd'hui, l'expansion se poursuit. Il semblerait même qu'elle s'accélère. Pour l'expliquer, on introduit la constante cosmologique, qui code "l'énergie du vide" et introduit une "pression négative"... Spéculation, quand tu nous tiens...

J'ai mis en gras les mots :Les galaxies sont toujours là car leur persistance sur une durée aussi longue est un mystère immense. TOUTES les simulations informatiques que l'on peut faire montrent qu'elles devraient se disperser en quelques centaines de millions d'années tout au plus. Mais il y a pire !

Sombre histoire

Dans les galaxies, les étoiles tournent chacune autour de leur centre de gravité commun, en quelque centaines de millions d'années. Grâce au merveilleux effet doppler, on peut mesurer cette vitesse de révolution : les étoiles qui s'éloignent de nous (à cause de leur rotation autour du noyau de la galaxie) sont plus décalées que la moyenne vers le rouge, et celles qui se rapprochent sont plus décalées vers le bleu. Ainsi on peut obtenir un graphe donnant la vitesse de révolution en fonction de la distance au noyau. Et là, catastrophe : les chiffres mesurés ne correspondent pas du tout aux calculs que l'on peut faire d'après la loi de Newton. Plus elles sont loin du noyau de la galaxie, plus les étoiles devraient tourner  lentement autour de ce noyau; Et ce n'est pas ce que l'on observe : près du coeur des galaxies, c'est effectivement le cas. Mais les étoiles périphériques, elles, tournent toutes à la même vitesse, quelle que soit leur distance au centre.

Jamais en reste, les théoriciens ont sortis de leur chapeau une explication fumeuse : il existerait, tout autour des galaxies, un halo immense de "matière sombre", invisible, dont l'attraction permettrait aux étoiles de suivre les trajectoires impossibles que l'on observe bel et bien. De quoi serait faite cette "matière sombre" ? Les spéculations vont bon train. Ce qui est intéressant, c'est que bien qu'on ne puisse pas la voir et qu'on ne sache pas de quoi elle pourrait bien être faite, on peut calculer la masse de cette matière "exotique". Et cette masse semblerait suffisante pour que l'univers soit fermée, pour nous conduire au "big crunch".

Je vous dirai plus loin ce que j'en pense. Mais ce n'est pas le seul problème !

Ça ne se dilate pas bien ...

En effet, le modèle standard nous dit que l'univers de dilate. MAIS LES GALAXIES NE PEUVENT PAS SE DILATER ! En effet tout d'abord les atomes ne peuvent pas se dilater, pour des raisons quantiques : leur taille est invariable, du moins si la constante de Planck l'est.  Donc les planètes ne peuvent pas se dilater. Et puis, en fait, tous les ensembles de corps liés par des liens gravitationnels (comme le système solaire, ou les galaxies) ne peuvent pas non plus se dilater car sinon leur stabilité serait gravement compromise en un rien de temps.

En fait, en reprenant l'image de l'univers-ballon qui se gonfle, il faut imaginer les galaxies comme des vignettes en papier collées sur le ballon, et qui ne se dilatent pas, elles, alors que l'espace entre elles semble le faire. Etrange, très étrange.

Qu'est-ce que c'est que cet univers qui se dilate tout en ne se dilatant pas ? Ceci constitue l'un des mystères les plus profonds de la cosmologie. Et la solution de ce paradoxe pourrait bien faire s'écrouler tout l'édifice. Je vous présenterai tout à l'heure une telle solution....

Pour l'heure on va attaquer de plein fouet les autres paradoxes du modèle standard... car il y en a d'autres !

> La suite : Paradoxes
< Page précédente : Petite histoire de l'univers