Les ibozoo-uu (2) : Poincaré entre en scène

Comment donner un sens à l'affirmation U. selon laquelle les axes d'un IU n'ont pas d'origine ? Il me semble que l'on peut donner un sens à cette affirmation en construisant une géométrie hyperbolique (donc définissant un cosmos à courbure négative) :

Connaissez vous le demi plan de Poincaré ? C'est une représentation d'un tel espace à courbure négative pour lequel on utilise une géométrie non euclidienne dite "hyperbolique" :

Dans une telle construction mathématique, on travaille sur un demi-plan ouvert correspondant à l'ensemble des points du plan dont la coordonnée y est strictement positive. Les "droites" dans cet espace sont soit des demi cercles dont len centre est sur l'axe horizontal soit des lignes verticales.

Ici A,B,C,D dont des "droites". D et C sont parallèles mais une droite peut avoir une infinité de parallèles passant par le meme point. En fait, deux droites peuvent être : secantes, assymptotes (elles se rejoignent à une de leur extrémité, cas de C et D) , ou parallèles (elles ont une perpendiculaire en commun).

Le fait que le demi-plan est ouvert montre que aucune droite n'a d'intersection avec cet axe. Ceci pourrait donc être un modèle pour les IU. Cette représentation est très utilisée en théorie du chaos (flots horocycliques, les "droite" modélisant des géodésiques).

Ici il y a tout un angle (hachuré sur la figure) où toutes les droites D passant par P sont parallèles à I (D et I ont une perpendiculaire commune Q)

Pour faire coller cette représentation à celle des IU, on "replie" notre demi plan de telle façcon que les coordonnées x+k.2pi soient l'une sur l'autre , de même pour y+n.2pi. On obtient alors un disque dont le point central est absent... ca ressemble de plus en plus à un IU !

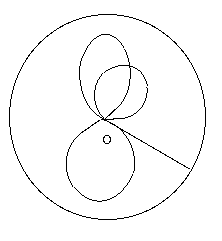Voici un demi-plan de Poincaré "replié en rond". L'axe des x est maintenant réduit au seul point O qui n'appartient pas à la figure, de mëme que le cercle extérieur qui représente y = infini. Nos droites sont alors soit des "rayons" du disque (y croit quand on s'éloigne vers le bord), soit des courbes bizaroïdes dont je n'ai pas cherché à expliciter l'equation.

Toujours est-il que l'on peut également définir des angles entre nos droites et que l'espace décrit continue à être hyperbolique...

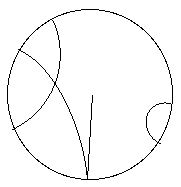En fait on aurait aussi pu procéder "à l'envers" en repliant l'axe horizontal du demi plan de Poincaré pour former le bord d'un disque, les "droites" ayant une origine sur le bord du disque :

Il faut noter que le point central n'existe pas (c'est le "point à l'infini") de même que le bord du disque (le disque est ouvert).

En réalité la tranformation la plus simple entre un cercle et un demi plan représenté par la partie supérieure du plan complexe est mathématiquement donnée par z -> i(1+z) / (1-z), qui transforme le disque unité en le demi-plan de poincaré. (en particulier le point z=(0,0) centre du disque se retrouve en i=(0,1).

L'inverse de cette transformation est, trivialement, z -> (z-i) / (z+i)

<a developper>