Les ibozoo-uu (3) : Univers angulaire
J'ai dit que chaque IU définit les coordonnées d'un point de l'espace-temps (muni d'une échelle). En fait ceci a des conséquences intéressantes.
Pour simplifier et pour commencer je supposerai que notre espace-temps n'a que deux dimensions, une dimension spatiale x et une dimension de temps t. Classiquement, on le modélise donc pa run plan, muni d'un axe X et d'un axe T.
Je ne procéderai pas ainsi : afin que les dimensions (x,t) restent des angles, je suppse que l'espace-temps est une sphére, les coordonnées (x,t) étant alors des angles permettant de se repérer sur la sphère. En fait, je courbe l'espace selon une sphère+. Ceci est ce que l'on fait en relativité, c'est du connu.
La nouveauté, c'est que nos coordonnées sont des angles et non des scalaires.
Pour
se repérer sur une sphère en coordonnées sphériques
il faut que l'une des coordonnées soit comprise entre 0 et 2pi (ou
-pi, +pi) , et l'autre entre 0 et pi (ou -pi/2, +pi/2) : c'est que l'on
fait pour se repérer sur la terre : longitude entre -180 et +180
degrès, latitude entre -90 et +90 degrès. Nous supposerons
ici que la longitude code le temps, et la latitude est la coordonée
X. C'est le contraire de ce qu'on fait d'habitude mais ce sera plus simple
quand nons parlerons de vitesses.
Mais ici nous avons un problème car les IU définissent des coordonnées x,t (x,y,z,t,e dans le cas général pentadimensionel) comprises entre 0 et 2pi : par exemple la longitude sera le temps : nous ferons donc varier ce temps entre 0 (début de l'univers) et 2pi (fin de l'univers, nous avons choisi une sphère a courbure positive, je sais mais c'est pour simplifier pour le moment ;-).
La coordonnée spatiale ne peut donc prendre des valeurs que entre 0 et pi pour coder des points sur la sphère ; mais les IU permettent de donner à x une valeur > pi : comment interpreter cela ? La réponse la plus simple serait que ces coordonnées x > pi codent en fait l'univers jumeau ! En fait on n'aurait pas une sphère mais deux, situèes aux même "endroit" (peu importe ce que cela veut dire !) ou si l'on préfère, une seule surface mais enroulée deux fois sur la sphère : un revètement a deux feuillets de notre sphère-cosmos.
Une autre possibilié serait que nous ayons non pas une sphère mais un tore : dans ce cas pas de pb, les deux coordonnées x et t sont entre 0 et 2pi.De plus le fait que le temps soit une des deux coordonnées, et surtout que ce soit maintenant un angle a des conséquences qui, elles, ne me semblent pas connues : par exemple si l'on dépasse la valeur t= 2pi que se passe-t-il ? on revient à t=0 ! Le temps reboucle sur lui-même !
Supposons donc un univers ne contenant qu'une seule particule, et suivant donc une géodésique de l'espace temps, en se déplaçant à vitesse constante. Représentons cela dans un repère cartésien (t,x) :
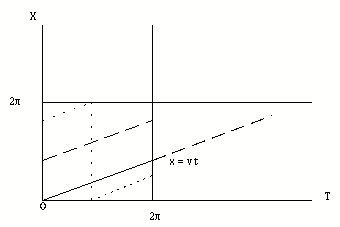Lorsque
le point se déplace en suivant x=vt, il finit par arriver en T=2pi
: sa trajectoire se "reboucle" alors... Le point finit en rebouclant par
atteindre "l'autre" frontière X=2pi, il reboucle alors en X=0 (trait
vertical pointillé) pour continuer ensuite... Le point de départ
est dans le schéma x=0, T=0 mais c'est tout a fait arbitraire, en
partant de n'importe quel autre point on aurait le même type de comportement.
Notons que dans le cas où l'univers n'est pas torique mais sphérique, le point passe dans l'univers jumeau chaque fois que x > pi , il repasse dans le premier feuillet lorsque x > 2pi. A priori, pour t donné ses coordonnées sont différentes.
Dans ce cas par exemple la trajectoire passe au point x (ou x + 2k.pi) aux instants t=((x + 2k.pi)/v) mod pi. La particule arrive donc en ces points en un temps nul (ou a une vitesse infinie), on peut donc dire qu'ils sont confondus...
En définitive notre point risque de parcourir tout l'espace-temps !
Minute ! ceci n'est vrai que si la vitesse v de la particule est irrationelle : dans ce cas en effet on peut démontrer que la particule passera arbitrairement près de tout point (x,t) donné. Mais si sa vitesse est un rationel p/q avec p/q entiers (que l'on peut prendre de telle façon que p^q=1) , alors il en va tout autrement :
Dès lors le point passe en x aux temps t=(x.q/p +2.pi.k.q/p) mod 2pi, soit pour p valeurs différentes données par k=0 à k=p-1. Notre point suit alors une trajectoire périodique :
Ici
on suppose toujours qu'on travaille en deux dimensions, une dimension d'espace
et une de temps, avec v = 2/3 : La trajectoire issue de O rencontre 2 =
2 pi en X = 2pi/3 ; elle "repart" alors de (T=0, x=2/3) jusqu'en (T=pi,
X=2pi) ; etc...
Dans le cas général ou v = p/q (avec p et q premiers entre eux) la trajectoire se replie pfois sur l'axe des temps et q fois sur l'axe des x. Les q points de l'axe des x (en T=0) qui sont touchés par la trajectoire sont donc "accédé" par la particule en un temps nul ; ces points sont confondus dans notre espace-temps. En fait il y a p.q domaines où le comportement dans chaque domaine est identique. (six dans notre exemple).
<a suivre>
> La suite des ibozoo-uu (4)> Autre suite : Synthèse de l'affaire Ummo
< retour aux pages "Ummo"
< retour aux pages "E.T."