Une nouvelle Géométrie (3) : Quantification
Résumé de l'épisode précédent :
Plus on veut simplifier : plus c'est compliqué !Cette page constitue le premier ingrédient de ma théorie géométrique.
Les Sapoints de Noël
Nous avons dit que lorsque la distance entre deux points valait zéro, il existait une incertitude angulaire de 360° sur la droite reliant ces deux points (confondus il est vrai !), mais que par contre dès que la distance différait de zéro, l'incertitude angulaire tombait, elle, à zéro.A l'évidence, ceci est peu satisfaisant : ne serait-il pas préférable d'avoir une incertitude sur l'angle qui décroisse avec la distance ? Après tout, ce c'est que suggère le sens commun : plus un objet est loin de moi, plus je peux le positionner angulairement avec précision :

On imagine donc de quantifier l'espace en le "pavant" avec des secteurs angulaires :
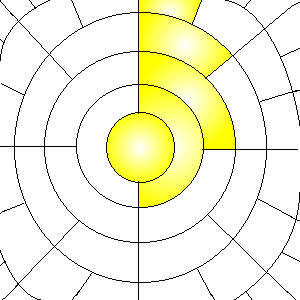
Sur la figure ci dessus, toutes les zones colorées (ou non) ont la même surface. Je propose d'appeler "SAPOINT" ou "spoint" un tel secteur angulaire et de garder le terme "point" pour l'espace euclidien. Il faut bien comprendre que ce réseau de couronnes concentriques n'est pas absolu, mais relatif : un tel réseau existe autour de chaque point euclidien).

Quelles sont les distances au centre correspondant à chaque couronne ? supposons que la rayon de la 1ière couronne (le sapoint central) soit 1 (les unités sont arbitraires). Alors, sa surface est pi. La seconde couronne inclut TROIS sapoints, celui du centre et les deux nouveaux secteurs qu'elle définit, la surface totale du cercle extérieur doit donc être 3pi ce qui fixe son rayon à racine(3) = 1.732..
La nième couronne inclut 2n-1 sapoints et son rayon est donc (2n-1)1/2.
Mais pourquoi as-tu choisi de diviser l'incertitude angulaire par deux à chaque étape ? Et pourquoi le sapoint central n'a-il que deux voisins, alors que les autres en ont quatre ou cinq ?Très bonnes questions, mon cher Watson : Mais avant de répondre il faut approfondir un peu ce que l'on entend par "zone d'incertitude autour d'un point M relativement à un point O" :
Dans le cas général, nous avons a priori deux manières
de considérer nos incertitudes de distances et d'angles :
la première est relative : On considère que, étant donné un point O de référence, tout autre point M est entouré d'une zone d'incertitude :

Le seconde est absolue : on se fixe un point O, une direction de référence et une échelle de référence (ceci revient à se fixer un second point de référence A) ; étant donné n'importe quel nombre N entier positif, on peut alors dessiner un réseau de N couronnes autour de O, chaque couronne n (n < N) étant divisée en k (n) secteurs angulaires. Dans l'exemple en haut de cette page, on avait pris k(n) = 2n-1.


En effet, comme l'incertitude angulaire diminue avec la distance OM, il peut arriver comme ci-dessus que M2 soit dans la zone d'incertitude de M1 alors que M1 n'est pas dans la zone d'incertitude de M2 ! Et on ne peux pas y parer par un "truc" du genre "je prends une zone d'incertitude autour du milieu du segment M1,M2" car il ne faut pas oublier que les incertitudes ne varient pas linéairement avec la distance OM, mais exponentiellement (ou même selon une loi générale qui reste à trouver). Je me trouve donc bien en peine de dire ou se trouve le milieu de M1M2, ni quelle est son incertitude angulaire et radiale... Mais on peut toujours essayer de prendre une sorte de moyenne "géométrique" : on suppose qu'étant donnée deux points M1 et M2 distincts de O, il existe une formule (à trouver) qui me donne un point M situé "entre" M1 et M2, tel que en traçant une zone d'incertitude (un sapoint) S autour de M on ait toujours soit M1 et M2 simultanément dans S, soit M1 et M2 simultanément en dehors de S :

Et si l'espace est courbe ?
Toutes ces histoires de Sapoints et d'incertitude, c'est bien joli,
mais ça ne mène nulle part... Je ne vois pas du tout où
tu veux en venir...
Un peu de patience, queue Diable ! ;-) Tu vas voir que la géométrie même de l'espace permet de définir les incertitudes !
Supposons en effet que, au lieu d'utiliser un plan comme dans les exemples ci dessus, nous tracions notre réseau de sapoints sur une sphère :


Première idée
En fait on découpe la sphère en tranches ou couronnes horizontales, parallèles à l'équateur, ayant même épaisseur angulaire A (différence de latitude) vues du centre. La "couronne" Nord (et celle Sud") sont en fait des calottes sphériques. Si N est le nombre de ces couronnes, alors leur épaisseur angulaire (différence de latitude) sera A = 180°/N, ou pi/N radians. (N= 8 dans la figure de gauche et 10 dans la figure de droite).Supposons que l'on numérote les couronnes de 1 à N-1, la 1ère couronne étant la calotte sphérique autour du pôle Nord. Sa surface est
S1 = 2 pi R2 (1-cos A) = 2 pi R2 (1-cos (pi/N))Supposons que nous prenions cette surface S1 comme unité. Alors il faut diviser chaque couronne en un certain nombre de "parts" dont chacune sera de surface unité. Ainsi tous nos sapoints seront définis et auront même surface.
Pour ce faire, il suffit que chaque calotte sphérique d'angle n x pi/N par rapport au pôle Nord ait une surface qui soit un nombre entier de fois celle de S1. En termes matheux , il faut calculer Sn /S1 : L'idée est que ce rapport, s'il est entier, ou tend vers un entier lorsque N -> oo, nous permettra de calculer facilement le nombre de sapoints de chaque couronne.
Sn = 2 pi R2 (1-cos (n x pi/N)) --> Sn/S1 = (1 -cos(n pi/N)) / (1 - cos (pi/N))Compte tenu de ce ce que cos x ~ 1 - x2 /2 + x4 / 4! - X6/ 6! + ...
Ce rapport tend vers n2 ( 1 - n2pi2/6N2 + n4pi4/180N4 - ... ) lorsque N -> oo et n << N
Nous avons donc un problème : bien que notre rapport puisse être rendu arbitrairement proche d'un entier, du moins pour de petits n (donc pas loin du pôle Nord) , il n'est pas entier pour des grands n, et autour du pôle Sud c'est sûrement la Bérézina, Trafalgar, Waterloo, Alesia !!
Mais Est-ce bien certain ? Non ! en effet pour de grands n, proches de N, (disons n = N - p, et 1 =< p << N), on a
cos (n pi/N) = cos ((N - p)pi / N) = cos (pi p / N). Génial !Autour du pôle Sud, tout se passe comme au pôle Nord et tout va bien.
Mais alors à l'équateur ? on a alors des n voisins de N/2 : (disons n = N/2 + p, pour fixer les idées) ; Dans ce cas on a
cos (pi n/N= cos (pi/2 + pi p/N) = - sin(pi p/N). ! Notre rapport Sn /S1 devient égal à
sin (pi p/N) / (1 - cos (pi/N))qui tend vers 2 p N / pi quand N -> oo. Ça n'a pas une tête d'entier...
Deuxième idée
Pourquoi nos couronnes devraient-elles avoir la même épaisseur angulaire ?Page en chantier

Désolé ! Sois patient...










