Une nouvelle Géométrie (2)
En principe vous devez avoir lu (1) avant d'arriver ici.Réflexions sur les réflexions
Dans la géométrie traditionnelle, tout part de la notion de "symétrie" : on considère les symétries par rapport à un point, ou symétries centrales, et les symétries par rapport à un axe ou un plan...Nous avons déjà vu qu'une symétrie centrale correspondant
à une rotation d'un angle pi : c'est vrai... mais en deux dimensions
seulement. Dans un espace à plus de deux dimensions, une symétrie
centrale a la curieuse propriété d'inverser la gauche et
la droite :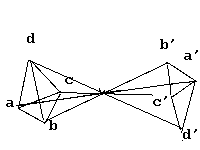
Aucune
rotation ne peut superposer a'b'c'd' et abcd. a'b'c'd' est l'image "en
miroir" de abcd : on dit que les deux objets sont énantiomorphes.
On appelle réflexion les symétries par rapport à un axe (en deux dimensions) ou un plan (en trois dimensions).
Dans un plan, on considérera les réflexions (symétries) par rapport à une droite, et dans l'espace les réflexions par rapport à un plan. L'image d'une figure par une réflexion est le symétrique de cette figure "de l'autre coté du miroir". cette notion de réflexion est la pierre d'angle de la géométrie axiomatique et de la notion de similitude :
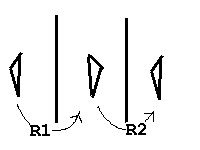
Une translation est ainsi par définition la composée
de deux réflexions selon des droites (resp. des plans) parallèles
:
De même une rotation est la composée de deux réflexions
selon des droites (resp des plans) qui se coupent :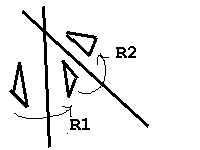
De
manière générale l'ensemble du groupe des isométries
peut être engendré par la composition d'au plus quatre réflexions.
Cette notion de réflexion permet de définir la notion d'orthogonalité : on dit que deux droites sont orthogonales lorsque l'une d'elle est l'image d'elle même par la réflexion prenant pour axe l'autre droite (et réciproquement, dirait Pierre Dac).
OK, mais lorsque l'espace n'est pas plat ? Bonne question, cher lecteur : dans ce cas nous n'avons plus des droites, mais seulement des géodésiques et une réflexion par rapport à une géodésique peut donner des choses bizarres, par ce que la notion d'orthogonalité ne peut plus être définie aussi simplement :
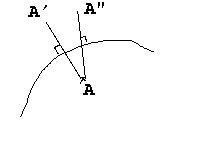A possède
deux images ! Impossible de définir une translation de cette manière,
semble-t-il...
Fausse piste ? Laissons cela en suspens pour le moment et intéressons nous encore une fois à la notion de distance :
Une tentative...
Dans la géométrie "classique" Riemannienne, le problème central est de définir la notion de distance sur une variété. On part de la notion de distance dans Rn, qui nous donne une notion de distance sur des nappes régulières (voir le document (1)), puis pour raccorder entre elles les nappes, on est conduit à une notion extrêmement complexe de tenseur métrique. Je ne veut pas entrer ici dans ces détails sordides, Il nous suffira de retenir que la notion de distance (métrique) est tout sauf triviale.Je vous propose d'avancer progressivement sur ce terrain difficile et miné en gardant notre point de vue "angulaire" sur la question :
Je suis donc en un point O, je peux voir un point A (la direction de mon regard suit une géodésique g), et je me pose la question de savoir comment déterminer la distance OA. Nous avons vu que cette distance n'est pas forcément unique, en effet il se peut dans certains cas que je puisse voir le point A dans plusieurs directions simultanément... Mais passons sur ce point pour l'instant, on peut en effet supposer que si A est "suffisamment" proche de moi alors l'espace mon voisinage est "suffisamment régulier" pour que je puise voir A dans une direction seulement (notons que ce postulat est en contradiction complète avec la mécanique quantique pour laquelle au contraire lorsque la distance devient très petite, l'espace temps devient de plus en plus "tordu", cette constatation est d'ailleurs une de mes motivation pour créer ma nouvelle géométrie...)
Supposons que dans une autre direction, je puisse voir un camarade C, dans la direction d'une géodésique h. Et supposons aussi que C voie A selon une géodésique j :
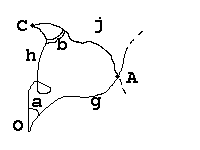Notons la
différence avec l'espace euclidien !
Pour moi (O) les géodésiques h et g font entre elles un angle a ; et C me dit qu'il voit un angle b entre les géodésiques h et j. Si je pose la "distance" OC comme unité, l'angle b peut fournir une mesure de la "distance" OA; lorsque b=0, A et O sont confondus. Il n'y a qu'un seul problème, c'est que la "distance" ainsi définie ne vérifie pas l'inégalité triangulaire ! Ce n'est donc pas une vraie distance...
En fait les "lignes d'isodistance à O" vont avoir une géométrie un rien bizarre...
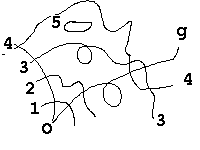On remarque
que à certains endroits la distance 3 est plus loin que la distance
4, et que la distance 5 n'existe que pour certains points...
Est ce que, au moins, lorsque je considère une variation infinitésimale
de l'angle b, définissant donc une géodésique j' "proche"
de j, le point A' d'intersection entre g et j' sera proche de A ? Rien
n'est moins sûr...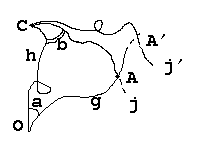
Quel
sac de noeuds ! (nb : on ne dit pas "un sac de noeuds" mais "un préservatif"
! ;-) Plus on tente d'y voir plus clair, moins on n'y voit plus goutte...
Retenons quand même qu'il semble y avoir, comme en théorie du chaos, un phénomène de dépendance sensitive des conditions initiales : une très faible variation de l'angle b peut conduire a deux "trajectoires" (géodésiques) très différentes, même si lorsque b -> 0 j tend vers j' et donc A- > A' en général (c'est à dire sauf cas particuliers "rares" (de mesure nulle, pour les pros)).
On peut faire une tentative pour récupérer notre notion de distance angulaire en "sortant du système", c'est à dire en plongeant notre surface (ou variété) dans un espace de dimension plus vaste :
Plongement
Et si nous prenions notre point C en dehors de la surface ? Supposons pour simplifier que notre surface est un plan. On peut alors définir une sphère de Riemann en un point P du plan :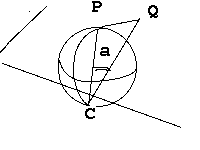
Les
point P et Q appartiennent au plan, C est en dehors. L'angle a = PCQ permet
de définir la distance PQ.
Oui mais si la surface n'est pas un plan, en particulier si elle est très "plissée", les choses sont moins simple (encore !) :
Voici une vue en coupe dans le plan CPQ :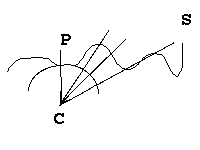 
Où
se trouve le point Q ? cela dépend : pour certains angles, on a
plusieurs points possibles... Et puis d'autre part qu'est ce que c'est
que ces "droites" (telles CP) sinon des géodésiques du sur-espace
? Ça complique encore le problème...
Notons que ce que nous avons fait, c'est :
La seconde opération peut se concevoir une comme rotation de
C hors de la surface , rotation selon un axe D ne passant pas par C (par
exemple on peut prendre un axe passant par O) :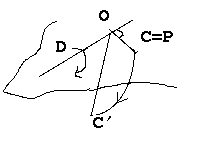 
Je
reviendrais plus loin sur cette opération de "rotation hors de la
surface".
La suite !
Assez de toutes ces salades ! viens-en au fait !Désolé, mais il me faut faire encore quelques digressions, ensuite c'est promis toutes les pièces du puzzle se mettront en place ! D'ailleurs tu as presque toutes les pièces en main...
La suite : Quantification